Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T19:27:39.306Z Has data issue: false hasContentIssue false
  • English
  • Français

Inversion of the Radon Transform on the Free Nilpotent Lie Group of Step Two

Published online by Cambridge University Press:  20 November 2018

Jianxun He  and
Jinsen Xiao
Jianxun He
Affiliation:
School of Mathematics and Information Sciences, Guangzhou University, Guangzhou 510006, China Key Laboratory of Mathematics and Interdisciplinary Sciences of Guangdong Higher Education Institutes, Guangzhou University, Guangzhou 510006, China. e-mail: [email protected], [email protected]
Jinsen Xiao*
Affiliation:
School of Mathematics and Information Sciences, Guangzhou University, Guangzhou 510006, China Key Laboratory of Mathematics and Interdisciplinary Sciences of Guangdong Higher Education Institutes, Guangzhou University, Guangzhou 510006, China. e-mail: [email protected], [email protected]
*
Corresponding author: Jinsen Xiao.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 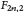${{F}_{2n,2}}$ be the free nilpotent Lie group of step two on $2n$ generators, and let $\mathbf{P}$ denote the affine automorphism group of 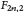${{F}_{2n,2}}$. In this article the theory of continuous wavelet transform on 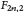${{F}_{2n,2}}$ associated with $\mathbf{P}$ is developed, and then a type of radial wavelet is constructed. Secondly, the Radon transform on 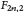${{F}_{2n,2}}$ is studied, and two equivalent characterizations of the range for Radon transform are given. Several kinds of inversion Radon transform formulae are established. One is obtained from the Euclidean Fourier transform; the others are from the group Fourier transform. By using wavelet transforms we deduce an inversion formula of the Radon transform, which does not require the smoothness of functions if the wavelet satisfies the differentiability property. In particular, if 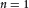$n\,=\,1$, 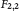${{F}_{2,2}}$ is the 3-dimensional Heisenberg group 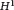${{H}^{1}}$, the inversion formula of the Radon transform is valid, which is associated with the sub-Laplacian on 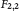${{F}_{2,2}}$. This result cannot be extended to the case 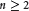$n\,\ge \,2$.

Keywords

43A8544A1252A38Radon transformwavelet transformfree nilpotent Lie groupunitary representationinversion formulasub-Laplacian
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 66 , Issue 3 , 01 June 2014 , pp. 700 - 720
Copyright
Copyright © Canadian Mathematical Society 2014

Footnotes

The authors are supported by the National Natural Science Foundation of China (Grant No. 10971039, 11271091).

References

[1] Benson, C. and Ratcliff, G., The space of bounded spherical functions on the free two-step nilpotent Lie group. Transform. Groups 13(2008), no. 2, 243–281. http://dx.doi.org/10.1007/s00031-008-9016-y Google Scholar
[2] Bröcker, T. and Dieck, T., Representations of compact Lie groups. Graduate Texts in Mathematics, 98, Springer-Verlag, New York, 1985.Google Scholar
[3] Domokos, A. and Franciullo, M. S., On the best constant for the Friedrichs-Knapp-Stein inequality in free nilpotent Lie groups of step two and applications to subelliptic PDE. J. Geom. Anal. 17(2007), no. 2, 245–252. http://dx.doi.org/10.1007/BF02930723 Google Scholar
[4] Felix, R., Radon-transformation auf nilpotenten Lie-Gruppen. Invent. Math. 112(1993), no. 2, 413–443. http://dx.doi.org/10.1007/BF01232441 Google Scholar
[5] Fischer, V., The bounded spherical functions on the free two-step nilpotent Lie group. J. Lie Theory 16(2006), no. 2, 351–370.Google Scholar
[6] Folland, G. B., Harmonic analysis in phase space. Annals of Mathematics Studies, 122, Princeton University Press, Princeton, NJ, 1989.Google Scholar
[7] Geller, D. and Stein, E. M., Singular convolution operators on the Heisenberg group. Bull. Amer. Math. Soc. 6(1982), no. 1, 99–103. http://dx.doi.org/10.1090/S0273-0979-1982-14977-1 Google Scholar
[8] He, J., An inversion formula of the Radon transform on the Heisenberg group. Canad. Math. Bull. 47(2004), no. 3, 389–397. http://dx.doi.org/10.4153/CMB-2004-038-9 Google Scholar
[9] He, J., A characterization of inverse Radon transform on the Laguerre hypergroup. J. Math. Anal. Appl. 318(2006), no. 1, 387–395. http://dx.doi.org/10.1016/j.jmaa.2005.05.069 Google Scholar
[10] Helgason, S., Integral geometry and Radon transforms. Springer, New York, 2011.Google Scholar
[11] Heymans, P., Pfaffians and skew-symmetric matrices. Proc. London Math. Soc. 19(1969), 730–768. http://dx.doi.org/10.1112/plms/s3-19.4.730 Google Scholar
[12] Holschneider, M., Inverse Radon transforms through inverse wavelet transforms. Inverse Problems 7(1991), no. 6, 853–861. http://dx.doi.org/10.1088/0266-5611/7/6/008 Google Scholar
[13] Jacobson, N., Lie algebras. Interscience Tracts in Pure and Applied Mathematics, 10, Interscience Publishers, New York-London, 1962.Google Scholar
[14] Liu, H. and Peng, L., Admissible wavelets associated with the Heisenberg group. Pacific J. Math. 180(1997), no. 1, 101–123. http://dx.doi.org/10.2140/pjm.1997.180.101 Google Scholar
[15] Muir, T., A treatise on the theory of determinants. Dover Publications, New York, 1960.Google Scholar
[16] Nessibi, M. M. and Trimèche, K., An inversion formula of the Radon transform on the Laguerre hypergroup by using generalized wavelets. J. Math. Anal. Appl. 208(1997), no. 2, 337–363. http://dx.doi.org/10.1006/jmaa.1997.5299 Google Scholar
[17] Peng, L. and Zhang, G., Radon transform on H-type and Siegel-type nilpotent group. Internat. J. Math. 18(2007), no. 9, 1061–1070. http://dx.doi.org/10.1142/S0129167X07004412 Google Scholar
[18] Rubin, B., Fractional integrals and potentials. Pitman Monographs and Surveys in Pure and Applied Mathematics, 82, Longman, Harlow, 1996.Google Scholar
[19] Rubin, B., The Calderón formula, windowed X-ray transforms and Radon transforms in Lp spaces. J. Four. Anal. Appl. 4(1998), no. 2, 175–197. http://dx.doi.org/10.1007/BF02475988 Google Scholar
[20] Rubin, B., The Radon transform on the Heisenberg group and the transversal Radon transform. J. Funct. Anal. 262(2012), no. 1, 234–272. http://dx.doi.org/10.1016/j.jfa.2011.09.011 Google Scholar
[21] Samko, S. G., Kilbas, A. A., and Marichev, O. I., Fractional integrals and derivatives. Theory and applications. Gordon and Breach Science Publishers, Yverdon, 1993.Google Scholar
[22] Stein, E. M., Harmonic analysis: real-variable methods, orthogonality, and oscillatory integrals. Princeton Mathematical Series, 43, Monographs in Harmonic Analysis, III. Princeton University Press, Princeton, NJ, 1993.Google Scholar
[23] Stein, E. M. and Weiss, G., Introduction to Fourier analysis on Euclidean spaces. Princeton Mathematical Series, No. 32. Princeton University Press, Princeton, NJ, 1971.Google Scholar
[24] Strichartz, R. S., Lp harmonic analysis and Radon transforms on the Heisenberg group. J. Funct. Anal. 96(1991), no. 2, 350–406. http://dx.doi.org/10.1016/0022-1236(91)90066-E Google Scholar
[25] Thangavelu, S., Harmonic analysis on the Heisenberg group. Progress in Mathematics, 159, Birkhäuser Boston Inc., Boston, MA, 1998.Google Scholar