We study the case of an Axiom $\text{A}$ holomorphic non-degenerate (hence non-invertible) map 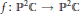$f:{{\mathbb{P}}^{2}}\mathbb{C}\to {{\mathbb{P}}^{2}}\mathbb{C}$, where 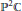${{\mathbb{P}}^{2}}\mathbb{C}$ stands for the complex projective space of dimension 2. Let 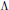$\Lambda $ denote a basic set for 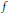$f$ of unstable index 1, and $x$ an arbitrary point of 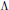$\Lambda $; we denote by 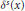${{\delta }^{s}}(x)$ the Hausdorff dimension of 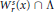$\text{W}_{r}^{s}(x) \cap \,\Lambda$, where $r$ is some fixed positive number and 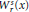$\text{W}_{r}^{s}(x)$ is the local stable manifold at $x$ of size 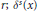$r;{{\delta }^{s}}(x)$ is called the stable dimension at$x$. Mihailescu and Urbański introduced a notion of inverse topological pressure, denoted by 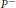${{P}^{-}}$, which takes into consideration preimages of points. Manning and McCluskey studied the case of hyperbolic diffeomorphisms on real surfaces and give formulas for Hausdorff dimension. Our non-invertible situation is different here since the local unstable manifolds are not uniquely determined by their base point, instead they depend in general on whole prehistories of the base points. Hence our methods are different and are based on using a sequence of inverse pressures for the iterates of 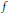$f$, in order to give upper and lower estimates of the stable dimension. We obtain an estimate of the oscillation of the stable dimension on 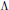$\Lambda $. When each point $x$ from 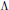$\Lambda $ has the same number 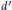${d}'$ of preimages in 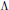$\Lambda $, then we show that 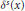${{\delta }^{s}}(x)$ is independent of $x$; in fact 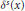${{\delta }^{s}}(x)$ is shown to be equal in this case with the unique zero of the map 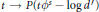$t\to P(t{{\phi }^{s}}-\log {d}')$. We also prove the Lipschitz continuity of the stable vector spaces over 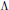$\Lambda $; this proof is again different than the one for diffeomorphisms (however, the unstable distribution is not always Lipschitz for conformal non-invertible maps). In the end we include the corresponding results for a real conformal setting.