Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
ahern, P. R.
and
Sarason, Donald
1967.
The Hp spaces of a class of function algebras.
Acta Mathematica,
Vol. 117,
Issue. 0,
p.
123.
1970.
Theory of Hp Spaces.
Vol. 38,
Issue. ,
p.
237.
Nikol'skii, N. K.
1976.
Invariant subspaces in the theory of operators and theory of functions.
Journal of Soviet Mathematics,
Vol. 5,
Issue. 2,
p.
129.
Hayashi, Mikihiro
1983.
Invariant subspaces on Riemann surfaces of Parreau-Widom type.
Transactions of the American Mathematical Society,
Vol. 279,
Issue. 2,
p.
737.
Waksman, Leonid
1987.
Commuting Nonselfadjoint Operators in Hilbert Space.
Vol. 1272,
Issue. ,
p.
39.
Yakubovich, D. V.
1989.
Toeplitz Operators and Spectral Function Theory.
Vol. 42,
Issue. ,
p.
305.
Yakubovich, D. V.
1992.
Invariant subspaces of the operator of multiplication by z in the space Ep in a multiply connected domain.
Journal of Soviet Mathematics,
Vol. 61,
Issue. 2,
p.
2046.
Aleman, Alexandru
and
Richter, Stefan
1996.
Simply invariant subspaces of H2 of some multiply connected regions.
Integral Equations and Operator Theory,
Vol. 24,
Issue. 2,
p.
127.
Fedorov, S. I.
1999.
On the angles between subspaces, the muckenhoupt condition, and projection from one co-invariant subspace onto another in the theory of character-automorphic hardy spaces on a multiply connected domain.
Journal of Mathematical Sciences,
Vol. 95,
Issue. 3,
p.
2276.
d'Avray, David
and
Menski, Werner
2012.
Authenticating Marriage: The Decree Tametsi in a Comparative Global Perspective.
SSRN Electronic Journal ,
Chen, Yanni
Hadwin, Don
Liu, Zhe
and
Nordgren, Eric
2018.
A Beurling Theorem for Generalized Hardy Spaces on a Multiply Connected Domain.
Canadian Journal of Mathematics,
Vol. 70,
Issue. 3,
p.
515.
Alpay, Daniel
Pinhas, Ariel
and
Vinnikov, Victor
2020.
de Branges spaces on compact Riemann surfaces and a Beurling-Lax type theorem.
Advances in Mathematics,
Vol. 373,
Issue. ,
p.
107315.
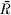 , analytic on R}.
, analytic on R}.