Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T00:44:22.241Z Has data issue: false hasContentIssue false
  • English
  • Français

Invariance of Torsion and the Borsuk Conjecture

Published online by Cambridge University Press:  20 November 2018

T. A. Chapman
T. A. Chapman*
Affiliation:
University of Kentucky, Lexington, Kentucky
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The following results of Whitehead and Wall are well-known applications of the algebraic K-theoretic functors K0 and K1 to basic homotopy questions in topology.

THEOREM 1 [20]. If f : X → Y is a homotopy equivalence between compact CW complexes, then there is a torsion τ(ƒ) in the algebraically-defined Whitehead group Wh π1(Y) which vanishes if and only if f is a simple homotopy equivalence.

THEOREM 2 [18]. If X is an arbitrary space which is finitely dominated (i.e., homotopically dominated by a compact polyhedron), then there is an obstruction σ(X) in the algebraically-defined reduced projective class group 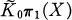which vanishes if and only if X is homotopy equivalent to some compact polyhedron.

If we direct sum over components, then the above statements make good sense even if the spaces involved are not connected.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 32 , Issue 6 , 01 December 1980 , pp. 1333 - 1341
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Bass, H., Algebraic K-theory (W. A. Benjamin, New York, 1969).Google Scholar
2. Bass, H., Heller, A., and Swan, R., The Whitehead group of a polynomial extension, Publ. I.H.E.S. Paris 22 (1964), 67–79.Google Scholar
3. Borsuk, K., Sur l'élimination de phenomènes paradox aux en topologie générale, Proc. Internat. Congr. Math., Vol. I, Amsterdam (1954), 197–208.Google Scholar
4. Chapman, T. A., Topological invariance of Whitehead torsion, Amer. J. Math. 96 (1974), 488–497.Google Scholar
5. Chapman, T. A., Cell-like mappings, Lecture Notes in Math. 482 (1973), 230–240.Google Scholar
6. Chapman, T. A., Homotopy conditions which detect simple homotopy equivalences, to appear in Pacific J. Math.CrossRefGoogle Scholar
7. Cohen, M., A course in simple-homotopy theory (Springer-Verlag, New York, 1970).Google Scholar
8. Dugundji, J., Topology (Allyn and Bacon, Boston, 1966).Google Scholar
9. Edwards, R. D., The topological invariance of simple homotopy type for polyhedra, preprint.CrossRefGoogle Scholar
10. Edwards, R. D., Siebenmanns variation of West's proof of the ANR theorem, manuscript.Google Scholar
11. Ferry, Steve, The homeomorphism group of a compact Hilbert cube manifold is an ANR, Annals of Math. 106 (1977), 101–119.Google Scholar
12. Ferry, Steve, Homotopy, simple homotopy, and compacta, preprint.Google Scholar
13. Quinn, Frank, Ends of maps, and applications, preprint.CrossRefGoogle Scholar
14. Milnor, J., On spaces having the homotopy type of a CW complex, Trans. A.M.S. 90 (1959), 272–280.Google Scholar
15. Milnor, J., Whitehead torsion, Bull. Amer. Math. Soc. 72 (1966), 358–426.Google Scholar
16. Siebenmann, L. C., A total Whitehead torsion obstruction, Comment. Math. Helv. 45 (1970), 1–48.Google Scholar
17. Spanier, E. H., Algebraic topology (McGraw-Hill, New York, 1966).Google Scholar
18. Wall, C. T. C., Finiteness conditions for CW complexes, Annals of Math. 81 (1965), 55–69.Google Scholar
19. West, J. E., Mapping Hilbert cube manifolds to ANRs, Annals of Math. 106 (1977), 1–18.Google Scholar
20. Whitehead, J. H. C., Simple homotopy types, Amer. J. Math. 72 (1950), 1–57.Google Scholar