Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-16T16:57:13.919Z Has data issue: false hasContentIssue false
  • English
  • Français

Intrinsic Functions on Matrices of Real Quaternions

Published online by Cambridge University Press:  20 November 2018

C. G. Cullen
C. G. Cullen*
Affiliation:
University of Pittsburgh
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is well known that any semi-simple algebra over the real field R, or over the complex field C, is a direct sum (unique except for order) of simple algebras, and that a finite-dimensional simple algebra over a field 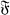is a total matrix algebra over a division algebra, or equivalently, a direct product of a division algebra over 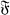and a total matrix algebra over 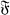(1). The only finite division algebras over R are R, C, and 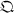, the algebra of real quaternions, while the only finite division algebra over C is C.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 15 , 1963 , pp. 456 - 466
Copyright
Copyright © Canadian Mathematical Society 1963

References

1. Albert, A. A., Structure of algebras, Amer. Math. Soc. Publications, 24 (1939).Google Scholar
2. Lee, H. C., Eigenvalues and canonical forms of matrices with quaternion coefficients, Proc. Roy. Irish Acad., Sect. A, 52 (1949), 253–260.Google Scholar
3. Rinehart, R. F., The equivalence of definition of a matrix function, Amer. Math. Monthly, 62 (1955), 395–413.Google Scholar
4. Rinehart, R. F., Elements of a theory of intrinsic functions on algebras, Duke Math. J., 27 (1960), 1–19.Google Scholar
5. Rinehart, R. F., Intrinsic functions on matrices, Duke Math. J., 28 (1961), 291–300.Google Scholar
6. Wiegmann, N. A., Some theorems on matrices with real quaternion elements, Can. J. Math., 7 (1955), 191–201.Google Scholar