Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T00:29:29.273Z Has data issue: false hasContentIssue false
  • English
  • Français

Intersections of Real Closed Fields

Published online by Cambridge University Press:  20 November 2018

Thomas C. Craven
Thomas C. Craven*
Affiliation:
University of Hawaii, Honolulu, Hawaii
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we wish to study fields which can be written as intersections of real closed fields. Several more restrictive classes of fields have received careful study (real closed fields by Artin and Schreier, hereditarily euclidean fields by Prestel and Ziegler [8], hereditarily Pythagorean fields by Becker [1]), with this more general class of fields sometimes mentioned in passing. We shall give several characterizations of this class in the next two sections. In § 2 we will be concerned with Gal 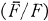, the Galois group of an algebraic closure F over F. We also relate the fields to the existence of multiplier sequences; these are infinite sequences of elements from the field which have nice properties with respect to certain sets of polynomials. For the real numbers, they are related to entire functions; generalizations can be found in [3].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 32 , Issue 2 , February 1980 , pp. 431 - 440
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Becker, E., Hereditarily Pythagorean fields and orderings of higher level, Lecture Notes, Institute* de Matemâtica Pura e Aplicada, Rio de Janeiro (1978).Google Scholar
2. Craven, T., Characterizing reduced Witt rings of fields, J. Algebr. 53 (1978), 68–77.Google Scholar
3. Craven, T. and Csordas, G., Multiplier sequences for fields, Illinois J. Math. 21 (1977), 801–817.Google Scholar
4. Diller, J. and Dress, A., Zur Galoistheorie pythagoreischer Korper, Arch. Math. 10 (1965), 148–152.Google Scholar
5. Endler, O., Valuation theory (Springer Verlag, New York, 1972).Google Scholar
6. Griffin, M., Galois theory and ordered fields, Queen's University Preprint (1972).Google Scholar
7. Lam, T. Y., The algebraic theory of quadratic forms (Benjamin, Reading, Mass., 1973).Google Scholar
8. Prestel, A. and Ziegler, M., Erblich euklidische Korper, J. Reine Angew. Math. 274/275 (1975), 196–205.Google Scholar
9. Ribenboim, P., Théorie des valuations (Les Presses de l'Université de Montréal, 1964).Google Scholar
10. Zariski, O. and Samuel, P., Commutative algebra, Vol. II (Van Nostrand, Princeton, NJ, 1960).Google Scholar