Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-22T22:52:17.154Z Has data issue: false hasContentIssue false
  • English
  • Français

Integral Representation of p-Class Groups In ℤp-Extensions and the Jacobian Variety

Published online by Cambridge University Press:  20 November 2018

Pedro Ricardo López-Bautista  and
Gabriel Daniel Villa-Salvador
Pedro Ricardo López-Bautista
Affiliation:
Departamento de Ciencias Básicas, Universidad Autónoma Metropolitana-Azcapotzalco, Av. San Pablo No. 180, Col. Reynosa Tamaulipas, Azcapotzalco D.F., C.P. 02200 México email: [email protected]
Gabriel Daniel Villa-Salvador
Affiliation:
Departamento de Matemáticas Centro de Investigación y de Estudios Avanzados, del I.P.N., Apartado Postal 14-740, 07000 México, D.F. email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For an arbitrary finite Galois $p$-extension 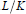$L/K$ of 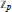${{\mathbb{Z}}_{p}}$-cyclotomic number fields of 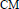$\text{CM}$-type with Galois group 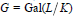$G=\text{Gal}(L/K)$ such that the Iwasawa invariants 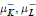$\mu _{K}^{-},\,\mu _{L}^{-}$ are zero, we obtain unconditionally and explicitly the Galois module structure of 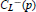$C_{L}^{-}\,(p)$, the minus part of the $p$-subgroup of the class group of $L$. For an arbitrary finite Galois $p$-extension 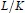$L/K$ of algebraic function fields of one variable over an algebraically closed field $k$ of characteristic $p$ as its exact field of constants with Galois group 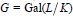$G=\text{Gal}(L/K)$ we obtain unconditionally and explicitly the Galois module structure of the $p$-torsion part of the Jacobian variety 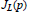${{J}_{L}}(p)$ associated to 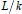$L/k$.

Keywords

11R3311R2311R5814H40ℤp-extensionsIwasawa’s theoryclass groupintegral representationfields of algebraic functionsJacobian varietyGalois module structure
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 50 , Issue 6 , 01 December 1998 , pp. 1253 - 1272
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Anderson, F.W. and Fuller, K.R., Rings and Categories of Modules. Graduate Texts in Math. 13, Springer-Verlag, Berlin-Heidelberg-New York, 1974.Google Scholar
2. Chevalley, C., Introduction to the Theory of Algebraic Functions of One Variable. Mathematical Surveys 6, Amer. Math. Soc., 1951.Google Scholar
3. Curtis, C.W. and Reiner, I., Methods of Representation Theory with Applications to Finite Groups and Orders, Vol. I. Pure and Appl. Math., Wiley-Interscience, New York, 1981.Google Scholar
4. Gold, R. and Madan, M. Galois representation of Iwasawa modules. Acta Arith. 46(1986), 243–255.Google Scholar
5. Iwasawa, K., On Γ-extensions of Algebraic Number Fields. Bull. Amer. Math. Soc. 65(1959), 183–226.Google Scholar
6. Iwasawa, K., On ℤ ℓ-extensions of Algebraic Number Fields. Ann. of Math. 98(1973), 246–326.Google Scholar
7. Iwasawa, K., Riemann-Hurwitz Formula and p-adic Galois Representation for Number Fields. Tôhoku Math. J. 33(1981), 263–288.Google Scholar
8. Karpilovsky, G., Group Representations, Vol. I. North-Holland Mathematics Studies 175, North-Holland, Amsterdam-London-New York-Tokyo, 1992.Google Scholar
9. López, R., Ph.D. Dissertation. Centro de Investigación y de Estudios Avanzados del I.P.N., February, 1998.Google Scholar
10. Nakajima, S., Equivariant Form of the Deuring- Šafarevič Formula for Hasse-Witt Invariants. Math. Z. 190(1985), 559–566.Google Scholar
11. Rzedowski, M., Villa, G. and Madan, M., Galois module structure of Tate modules. Math. Z. 224(1997), 77–101.Google Scholar
12. Sehgal, Sudarshan K., Topics in Group Rings. Pure and Appl. Math. 50, Marcel Dekker, Inc., New York, 1978.Google Scholar
13. Serre, J.P., Local Fields, Graduate Texts in Math. 67, Springer-Verlag, New York, 1979.Google Scholar
14. Serre, J.P., Algebraic Groups and Class Fields. Graduate Texts in Math. 117, Springer-Verlag, Berlin- Heidelberg-New York, 1988.Google Scholar
15. Suzuki, M., Group Theory I. Grundlehren Math. Wiss. 247, Springer-Verlag, Berlin-Heidelberg-New York, 1980.Google Scholar
16. Valentini, R., Some p-adic Galois Representations for Curves in Characteristic p. Math. Z. 192(1986), 541–545.Google Scholar
17. Villa, G. and Madan, M., Structure of Semisimple Differentials and p-Class Groups in ℤ p-extensions. Manuscripta Math. 57(1987), 315–350.Google Scholar
18. Villa, G., Integral representations of p-class groups in ℤ p-extensions, semisimple differentials and Jacobians. Arch.Math. 56(1991), 254–269.Google Scholar