No CrossRef data available.
Article contents
Integral Representation for U3 × GL2
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Gelbart and Piatetskii-Shapiro constructed various integral representations of Rankin–Selberg type for groups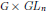 
$G\,\times \,G{{L}_{n}}$, where 
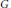$G$ is of split rank 
$n$. Here we show that their method can equally well be applied to the product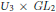 
${{U}_{3}}\,\times \,G{{L}_{2}}$, where 
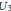${{U}_{3}}$ denotes the quasisplit unitary group in three variables. As an application, we describe which cuspidal automorphic representations of 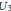${{U}_{3}}$ occur in the Siegel induced residual spectrum of the quasisplit 
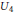${{U}_{4}}$.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2009
References
[1]
Casselman, W. and Shalika, J., The unramified principal series of p-adic groups. II. The Whittaker function.
Compositio Math.
41(1980), no. 2, 207–231.Google Scholar
[2]
Flicker, Yuval Z., On distinguished representations. J. Reine Angew. Math. 418(1991), 139–172.Google Scholar
[3]
Gelbart, S. and Piatetski-Shapiro, I., Automorphic forms and L-functions for the unitary group. In: Lie Group Representations. Lecture Notes in Math. 1041, Springer, Berlin, 1984, pp. 141–184.Google Scholar
[4]
Gelbart, S., Piatetski-Shapiro, I., and Rallis, S., Explicit constructions of automorphic L-functions.
Lecture Notes in Mathematics 1254, Springer-Verlag, Berlin, 1987.Google Scholar
[5]
Gelbart, S., Rogawski, J., and Soudry, D., Endoscopy, theta-liftings, and period integrals for the unitary group in three variables.
Ann. of Math. (2)
145(1997), no. 3, 419–476.Google Scholar
[6]
Gelbart, Shahidi, Analytic Properties of Automorphic L-functions.
Lecture Notes in Mathematics, No.
1254, Springer Verlag, 1987.Google Scholar
[7]
Gross, B. H. and Prasad, D., On the decomposition of a representation of
SOn when restricted to SOn−1. Canad. J. Math.
44(1992), no. 5, 974–1002.Google Scholar
[8]
Harder, G., Langlands, R. P., and Rapoport, M., Algebraische Zyklen auf Hilbert-Blumenthal-Flächen.
J. Reine Angew. Math.
366(1986), 53–120.Google Scholar
[9]
Jacquet, H., I. I. Piatetskii-Shapiro, and Shalika, J. A., Rankin-Selberg convolutions.
Amer. J. Math.
105(1983), no. 2, 367–464.Google Scholar
[10]
Jacquet, H. and Shalika, J. A., On Euler products and the classification of automorphic representations. I. Amer. J. Math. 103(1981), no. 3, 499–558.Google Scholar
[11]
T., Kon-No, The residual spectrum of
U(2, 2). Trans. Amer. Math. Soc.
350(1998), no. 4, 1285–1358.Google Scholar
[12]
Koseki, H., and Oda, T., Whittaker functions for the large discrete series representations of SU(2, 1) and related zeta integrals. Publ. Res. Inst. Math. Sci. 31(1995), no. 6, 959–99.Google Scholar
[13]
Moeglin, C. and Waldspurger, J.-L., Spectral decomposition and Eisenstein series.
Cambridge Tracts in Mathematics 113, Cambridge University Press, Cambridge, 1995. Une paraphrase de l’Écriture [A paraphrase of Scripture].Google Scholar
[14]
Rogawski, J. D., Automorphic representations of unitary groups in three variables.
Annals of Mathematics Studies 123, Princeton University Press, Princeton, NJ, 1990.Google Scholar
[15]
Soudry, D., Rankin–Selberg convolutions for SO2l+1 × GLn : Local Theory. Mem. Amer. Math. Soc. 500(1993).Google Scholar
[16]
Soudry, D.
On Langlands functoriality from classical groups to GLn. Astérisque 298 (2005), 335–390.Google Scholar
[17]
Watanabe, T., A comparison of automorphic L-functions in a theta series lifting for unitary groups.
Israel J. Math.
116(2000), 93–116.Google Scholar
[18]
S.-W., Zhang, Gross-Zagier formula for GL(2). II. In: Heegner points and Rankin L-series, Math. Sci. Res. Inst. Publ. 49, Cambridge Univ. Press, Cambridge, 2004, pp. 191–214.Google Scholar
You have
Access