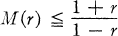Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Twomey, J. B.
1983.
On certain sums of Fourier-Stieltjes coefficients.
Transactions of the American Mathematical Society,
Vol. 280,
Issue. 2,
p.
611.
Girela, Daniel
1989.
Integral means of univerlent functions with restricted Hayman index.
Israel Journal of Mathematics,
Vol. 65,
Issue. 1,
p.
44.
Twomey, J. Brian
2008.
The Modulus of Continuity of a Measure with Finite Energy.
Computational Methods and Function Theory,
Vol. 8,
Issue. 1,
p.
47.


 the class of functions of the form
the class of functions of the form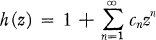
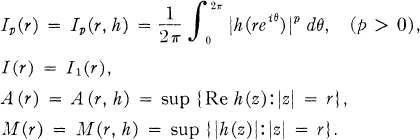
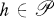 , the inequality
, the inequality