Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T00:24:23.462Z Has data issue: false hasContentIssue false
  • English
  • Français

Injectives and Projectives in Term Finite Varieties of Algebras

Published online by Cambridge University Press:  20 November 2018

George F. McNulty ,
T. Nordahl  and
H. E. Scheiblich
George F. McNulty
Affiliation:
University of South Carolina, Columbia, South Carolina
T. Nordahl
Affiliation:
Medical University of South Carolina, Charleston, South Carolina
H. E. Scheiblich
Affiliation:
Medical University of South Carolina, Charleston, South Carolina
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

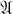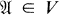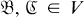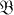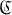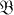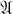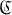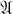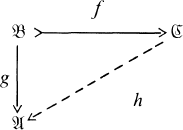
Let V be a class of similar algebras. An algebra is V-injective provided and whenever and fis a one-to-one homomorphism from into and g is a homomorphism from into , then there is a homomorphism h from into such that h º f = g. So 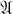is injective provided all diagrams of the following sort can be completed.

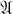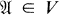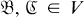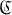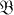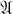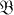Dually, is V-projective provided and whenever and f is a homomorphism from onto and g is a homomorphism from into , then there is a homomorphism h from 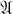into 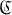such that f º h = g. So is projective provided all diagrams of the following sort can be completed:

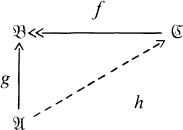
This usage of the words “projective” and “injective” differs somewhat from the usage current in category theory.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 35 , Issue 5 , 01 October 1983 , pp. 769 - 775
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. R., Balbes, Projective and injective distributive lattices, Pacific J. Math 21 (1967), 405–420.Google Scholar
2. G., Bruns and H., Lakser, Injective hulls of semilattices, Can. Math. Bull. 13 (1970), 115–118.Google Scholar
3. L., Calabi, A semigroup is free iff it is projective, Notices of Amer. Math. Soc. 13 (1966), 720.Google Scholar
4. A., Day, Injectives in non-distributive equational classes of lattices are trivial, Archiv der Math. 21 (1970), 113–115.Google Scholar
5. A., Day, Injectivity in equational classes of algebras, Can. J. Math. 24 (1972), 209–220.Google Scholar
6. R., Freese and J. B., Nation, Projective lattices, Proc. Amer. Math. Soc. 77 (1979), 174–178.Google Scholar
7. J. A., Gerhard, Injectives in equational classes of idempotent semigroups, Semigroup Forum 9 (1974), 36–53.Google Scholar
8. P., Grillet, On free commutative semigroups, J. Natural Sciences and Mathematics 9 (1969), 71–78.Google Scholar
9. P., Halmos, Injective and projective Boolean algebras, Proc. Sympos. Pure Math. 11 (1961), 114–122.Google Scholar
10. A., Horn and Kimura, , The category of semilattices, Algebra Universalis a (1971), 26–38.Google Scholar
11. N., Jacobson, Basic algebra, II (W. H. Freeman and Company, San Francisco, 1980), 666 + xix.Google Scholar
12. G., McNulty, The decision problem for equational bases of algebras, Ann. Math. Logic 12 (1977), 193–259.Google Scholar
13. G., McNulty, Structural diversity in the lattice of equational theories, Algebra Universalis, to appear.Google Scholar
14. G., McNulty, Covering in the lattice of equational theories and some properties of term finite theories, Algebra Universalis, to appear.Google Scholar
15. T., Nordahl and H. E., Scheiblich, Projective bands, Algebra Universalis 11 (1980), 139–148.Google Scholar
16. G., Pollak, On the existence of covers in the lattice of varieties, in Contributions to General Algebra, Proc. Conf. Klagenfurt (1978), 235–247, (Verlag Johannes Heyn Klagenfurt, 1979).Google Scholar
17. B. M., Schein, Injectives in certain classes of semigroups. Semigroup Forum 9 (1974), 159–171.Google Scholar
18. B. M., Schein, On Wo papers of B. M. Schein. 23 (1981), 87–89.Google Scholar
19. W., Taylor, Some constructions of compact algebras, Ann. Math. Logic 36 (1971), 395–435.Google Scholar
20. A., Trahtman. Covering elements in the lattice of varieties of algebras. (Russian), Mat. Zametki 75 (1974), 304–312.Google Scholar