Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-12T08:52:40.613Z Has data issue: false hasContentIssue false
  • English
  • Français

Inflection Points of Bessel Functions of Negative Order

Published online by Cambridge University Press:  20 November 2018

Lee Lorch ,
Martin E. Muldoon  and
Peter Szego
Lee Lorch
Affiliation:
Department of Mathematics and Statistics, York University, North York, Ontario M3J 1P3
Martin E. Muldoon
Affiliation:
Department of Mathematics and Statistics, York University, North York, Ontario M3J 1P3
Peter Szego
Affiliation:
75 Glen Eyrie Ave., San Jose, California 95125, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the positive zeros j″vk, k = 1, 2,…, of the second derivative of the Bessel function Jν(x). We are interested first in how many zeros there are on the interval (0,jν1), where jν1 is the smallest positive zero of Jν(x). We show that there exists a number ƛ = —0.19937078… such that 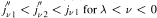and 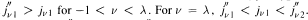. Moreover, j″v1 decreases to 0 and j″ν2 increases to j″01 as ν increases from ƛ to 0. Further, j″vk increases in —1 < ν< ∞, for k = 3,4,… Monotonicity properties are established also for ordinates, and the slopes at the ordinates, of the points of inflection when — 1 < ν < 0.

Keywords

33A4034B30Bessel functionszerosinflection points
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 43 , Issue 6 , 01 December 1991 , pp. 1309 - 1322
Copyright
Copyright © Canadian Mathematical Society 1991

References

1. Abramowitz, M., Zeros of certain Bessel functions of fractional order, Math. Tables and other Aids to Comp. (now Math. Comp.) 1(1953), 353–354.Google Scholar
2. Elbert, Á., Some inequalities concerning Bessel functions of first kind, Studia Sci. Math. Hungar. 6( 1971 ), 277–285.Google Scholar
3. Elbert, Á. and Laforgia, A., On the square of the zeros of Bessel functions, SIAM J. Math. Anal. 15( 1984), 206–212.Google Scholar
4. Erdélyi, A., et al., Higher Transcendental Functions, vol. 2. McGraw-Hill, New York, 1953.Google Scholar
5. Ifantis, E.K., Kokologiannaki, C.G. and Kouris, C.B., On the positive zeros of the second derivative of Bessel functions, J. Comput. Appl. Math. 34(1991), 21–31.Google Scholar
6. Kerimov, M.K. and Skorokhodov, S.L., Calculation of the multiple zeros of the derivatives of the cylindrical Bessel functions Jv (z) and Yv(z), USSR Comput. Maths. Math. Phys. (6)25(1985), 101-107.[Trans, from Zh. vychisl. Mat. mat. Fiz. (12)25(1985), 1749–1760..Google Scholar
7. Kerimov, M.K., Multiple zeros of derivatives of cylindrical Bessel functions, Soviet Math. Dokl. 33( 1986), 650-653.[Trans, from Dokl. Akad. Nauk. SSSR (2)288(1986), 285–288..Google Scholar
8. Lorch, L., Muldoon, M.E. and Szego, P., Higher monotonicity properties of certain Sturm-Liouville functions, IV, Canad. J. Math. 24(1972), 349–368.Google Scholar
9. Lorch, L. and Szego, P., On the zeros of derivatives of Bessel functions, SIAM J. Math. Anal. 19(1988), 1450–1454.Google Scholar
10. Lorch, L. and Szego, P., On the points of inflection of Bessel functions of positive order, I, Canad. J. Math. 42( 1990), 933–948. ibid. 1132.Google Scholar
11. Szegö, G., Orthogonal Polynomials. 4th éd., Amer. Math. Soc. Colloquium Publications, 23, Providence, 1975.Google Scholar
12. Watson, G.N., A Treatise on the Theory of Bessel Functions. 2nd éd., Cambridge University Press, 1944.Google Scholar
13. Wong, R. and Lang, T., On the points of inflection of Bessel functions of positive order, II, Canad. J. Math. 43(1991)628–651.Google Scholar