Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-29T14:37:58.489Z Has data issue: false hasContentIssue false
  • English
  • Français

Infinite Systems of Differential Equations II

Published online by Cambridge University Press:  20 November 2018

J. P. McClure  and
R. Wong
J. P. McClure
Affiliation:
University of Manitoba, Winnipeg, Canada
R. Wong
Affiliation:
University of Manitoba, Winnipeg, Canada
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper is a continuation of earlier work [6], in which we studied the existence and the stability of solutions to the infinite system of nonlinear differential equations

(1.1)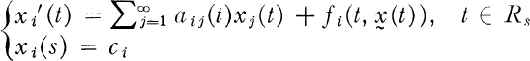

i = 1, 2, …. Here s is a nonnegative real number, Rs = {t ∈ R: t ≧ s}, and 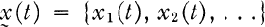denotes a sequence-valued function. Conditions on the coefficient matrix A(t) = [aij(t)] and the nonlinear perturbation 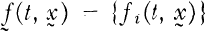were established which guarantee that for each initial value c= {ct} ∈ l1, the system (1.1) has a strongly continuous l1valued solution x(t) (i.e., each 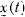is continuous and 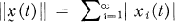converges uniformly on compact subsets of Rs). A theorem was also given which yields the exponential stability for the nonlinear system (1.1).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 31 , Issue 3 , 01 June 1979 , pp. 596 - 603
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Avramescu, C., Sur l'existence des solutions convergentes des systèmes d1 équations différentielles non linéaires, Ann. Mat. pura appl., 4 (81) (1969), 147–168.Google Scholar
2. Bellman, R., The boundedness of solutions of infinite systems of linear differential equations, Duke Math. J., 14 (1947), 695–706.Google Scholar
3. Bridgland, J. F. Jr., Asymptotic behavior of the solutions of nonlinear differential equations, Proc. Amer. Math. Soc. 13 (1962), 373–377.Google Scholar
4. Coppel, W. A., Stability and asymptotic behavior of differential equations (Heath Math. Monographs, Boston, 1965).Google Scholar
5. Friedman, A., Partial differential equations (Holt, Rinehart and Winston, New York, 1969).Google Scholar
6. McClure, J. P. and Wong, R., Infinite systems of differential equations, Can. J. Math.. 28 (1976), 1132–1145.Google Scholar
7. Shaw, L., Solutions for infinite-matrix differential equations, j. Math. Anal. Appl. 41 (1973), 373–383.Google Scholar