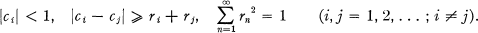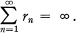Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wilker, John B.
1967.
Open Disk Packings of a Disk.
Canadian Mathematical Bulletin,
Vol. 10,
Issue. 3,
p.
395.
Wilker, J. B.
1969.
Four Proofs of a Generalization of the Descartes Circle Theorem.
The American Mathematical Monthly,
Vol. 76,
Issue. 3,
p.
278.
Melzak, Z. A.
1969.
On the solid-packing constant for circles.
Mathematics of Computation,
Vol. 23,
Issue. 105,
p.
169.
KAUSCH-BLECKEN, H. H.
SCHMELING, VON
and
TSCHOEGL, N. W.
1970.
Osculatory Packing of Finite Areas with Circles.
Nature,
Vol. 225,
Issue. 5238,
p.
1119.
Boyd, David W.
1970.
Osculatory Packings by Spheres.
Canadian Mathematical Bulletin,
Vol. 13,
Issue. 1,
p.
59.
Boyd, David W.
1970.
Lower bounds for the disk packing constant.
Mathematics of Computation,
Vol. 24,
Issue. 111,
p.
697.
Baranovskii, E. P.
1971.
Progress in Mathematics.
p.
209.
Boyd, David W.
1971.
The disk-packing constant.
Aequationes Mathematicae,
Vol. 7,
Issue. 2-3,
p.
182.
Boyd, David W.
1972.
Disk Packings which have Non-Extreme Exponents.
Canadian Mathematical Bulletin,
Vol. 15,
Issue. 3,
p.
341.
Boyd, David W.
1973.
The residual set dimension of the Apollonian packing.
Mathematika,
Vol. 20,
Issue. 2,
p.
170.
Crittenden, Richard B.
and
Swanson, Leonard G.
1976.
An Elementary Proof that the Unit Disc is a Swiss Cheese.
The American Mathematical Monthly,
Vol. 83,
Issue. 7,
p.
552.
Wilker, J. B.
1977.
Sizing up a solid packing.
Periodica Mathematica Hungarica,
Vol. 8,
Issue. 2,
p.
117.
Wilker, J. B.
1981.
The Geometric Vein.
p.
379.
Boyd, David W.
1982.
The sequence of radii of the Apollonian packing.
Mathematics of Computation,
Vol. 39,
Issue. 159,
p.
249.
Sarin, Subhash C.
1983.
The Mixed Disc Packing Problem: Part I: Some Bounds on Density.
IIE Transactions,
Vol. 15,
Issue. 1,
p.
37.
Tricot, Claude
1984.
A new proof for the residual set dimension of the apollonian packing.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 96,
Issue. 3,
p.
413.
Tricot, Claude
1989.
Porous surfaces.
Constructive Approximation,
Vol. 5,
Issue. 1,
p.
117.
Tricot, Claude
1989.
Constructive Approximation.
p.
117.
Bullett, S
and
Mantica, G
1992.
Group theory of hyperbolic circle packings.
Nonlinearity,
Vol. 5,
Issue. 5,
p.
1085.
Moraal, H
1994.
Apollonian arrangements of spheres in d-dimensional space.
Journal of Physics A: Mathematical and General,
Vol. 27,
Issue. 23,
p.
7785.
 are the same. If rn is the radius of Dn and the complex number cn represents its centre, then the conditions for C to be a packing are
are the same. If rn is the radius of Dn and the complex number cn represents its centre, then the conditions for C to be a packing are