Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T01:02:08.016Z Has data issue: false hasContentIssue false
  • English
  • Français

Inequalities and Inverse Theorems in Restricted Rational Approximation Theory

Published online by Cambridge University Press:  20 November 2018

Peter Borwein
Peter Borwein*
Affiliation:
University of British Columbia, Vancouver, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The following lemma, part a) due to S. N. Bernstein and part b) due to A. A. Markov, is fundamental to the proofs of many inverse theorems in polynomial approximation theory.

LEMMA 1. [2, p. 62 and p. 67] Let ∏n denote the real polynomials of degree at most n. Let p ∈ ∏n, then

a)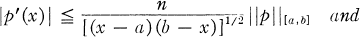

b)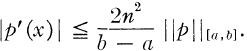

From the lemma one can deduce, for example:

THEOREM 1. Iƒ there is a sequence of polynomials pn ∈ ∏n and a δ > 0 so that ‖f – pn‖[a, b] ≧ A/nk + δ then f is k times continuously differentiate on (a, b).

We shall refer to inequalities, such as those of Lemma 1 that bound the derivative r′ of a rational function of degree n in terms of its supremum norm ‖r‖[a, b] and n, as Bernstein-type inequalities.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 32 , Issue 2 , February 1980 , pp. 354 - 361
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Lorentz, G. G., Approximation of functions (Holt, Rinehart and Winston, New York, 1966).Google Scholar
2. Meinardus, G., Approximation of functions: Theory and numerical methods (Springer-Verlag, New York, 1967).Google Scholar