Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T00:45:28.015Z Has data issue: false hasContentIssue false
  • English
  • Français

Inclusion Theorems for FX-Spaces

Published online by Cambridge University Press:  20 November 2018

Johann Boos
Johann Boos*
Affiliation:
Fernuniversität-Gesamthochschule, Hagen, Federal Republic of Germany
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The main result of this paper is Theorem 1 (in connection with Corollary 1 (e)), which says that the implication

*

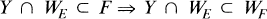
holds for every separable FK-space F, for every FK-space E containing φ and for certain (for example, solid) FK-AB-spaces Y. At this, φ denotes the space of all finite sequences and WE is the set of all elements of E being weakly sectionally convergent.

This result was proved by Bennett and Kalton ([1] and [3]) in the special case that E contains all null sequences and that Y is the space m of all bounded sequences or the space of all sequences almost converging to zero.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 39 , Issue 3 , 01 June 1987 , pp. 631 - 645
Copyright
Copyright © Canadian Mathematical Society 1987

References

1. Bennett, G. and Kalton, N. J., FK-spaces containing c0 , Duke Math. J. 39 (1972), 561–582.Google Scholar
2. Bennett, G. and Kalton, N. J., Inclusion theorems for K-spaces, Can. J. Math. 25 (1973), 511–524.Google Scholar
3. Bennett, G. and Kalton, N. J., Consistency theorems for almost convergence, Trans Amer. Math. Soc. 198 (1974), 23–43.Google Scholar
4. Boos, J., Verträglichkeit von konvergenztreuen Matrixverfahren, Math. Z. 128 (1972), 15–22.Google Scholar
5. Boos, J. and Leiger, T., Sätze vom Mazur-Orlicz-Typ, Studia Math. 81 (1985), 71–85.Google Scholar
6. Brudno, A. L., Summation of bounded sequences by matrices, Math. Sbornik, n. Ser. 16 (1945), 191–247.Google Scholar
7. Duran, J. P., Infinite matrices and almost convergence, Math. Z. 128 (1972), 75–83.Google Scholar
8. Mazur, S. and Orlicz, W., Sur les méthodes linéaires de sommation, C. R. Acad. Sci. Paris 196 (1933), 32–34.Google Scholar
9. Mazur, S. and Orlicz, W., On linear methods of summability, Studia Math. 14 (1955), 129–160.Google Scholar
10. Snyder, A. K., Consistency theory in semiconservatice spaces, Studia Math. 71 (1982), 1–13.Google Scholar
11. Volkov, I. I., Über die Verträ;glichkeit zweier Summationsmethoden, Mat. Zametki 1 (1967), 283–290.Google Scholar
12. Wilansky, A., Distinguished subsets and summability invariants, J. Analyse Math. 12 (1964), 327–350.Google Scholar
13. Wilansky, A., Summability through functional analysis (Amsterdam-New York-Oxford: North Holland, 1984).Google Scholar