Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T13:39:14.255Z Has data issue: false hasContentIssue false
  • English
  • Français

Incidence Relations in MulticoherentSpaces II

Published online by Cambridge University Press:  20 November 2018

A. H. Stone
A. H. Stone*
Affiliation:
Manchester University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Introduction. One standard method of studying the incidences of a system of sets A 1, A2, .… , An is to consider the nerve 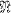of the system. However, this gives no direct information as to the numbers of components of the various intersections of the sets—information which would be desirable in several geometrical problems. The object of the present paper is to modify the definition of the nerve so that these numbers of components can be taken into account, and to study this modified nerve 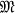for systems of sets in a connected, locally connected, normal T1 space S of a given degree of multicoherence r(S). The principal result (Theorem 6, 6.4) is a refinement of a theorem of Eilenberg [4, p. 107], and asserts that, if 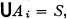then under suitable hypotheses we have

(1)

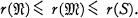
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 2 , 1950 , pp. 461 - 480
Copyright
Copyright © Canadian Mathematical Society 1950

References

[1] Dowker, C. H., Mapping theorems for non-compact spaces, Amer. J. Math., vol. 69 (1947), pp. 200–242.Google Scholar
[2] Eilenberg, S., Transformations continues en circonférence et la topologie du plan, Fund. Math., vol. 26 (1936), pp. 61–112.Google Scholar
[3] Eilenberg, S., Sur les espaces multicohérents I, Fund. Math., vol. 27 (1936), pp. 153–190.Google Scholar
[4] Eilenberg, S., Sur les espaces multicohérents II, Fund. Math., vol. 29 (1937), pp. 101–122.Google Scholar
[5] Eilenberg, S., Sur la multicohérence des surfaces closes, Comptes Rendus de 1' Académie des Sciences de Warsaw, vol. 30 (1937), pp. 109–111.Google Scholar
[6] Lefschetz, S., Algebraic Topology, Amer. Math. Soc. Colloquium Publications, vol. 27 (1942).Google Scholar
[7] Lefschetz, S., Topics in Topology, Ann. of Math. Studies No. 10, Princeton, 1942.Google Scholar
[8] Seifert, H. and Threlfall, W., Lehrbuch der Topologie (Leipzig, 1934).Google Scholar
[9] Stone, A. H., Incidence relations in unicoherent spaces, Trans. Amer. Math. Soc, vol. 65 (1949), pp. 427–447.Google Scholar
[10] Stone, A. H., Incidence relations in multicoherent spaces, I, Trans. Amer. Math. Soc, vol. 66 (1949), pp. 389–406.Google Scholar
[11] Wallace, A. D., Separation spaces, Ann. of Math., vol. 42 (1941), pp. 687–697.Google Scholar
[12] Whyburn, G. T., Analytic Topology, Amer. Math. Soc. Colloquium Publications, vol. 28 (1942).Google Scholar