No CrossRef data available.
Article contents
Immersions of Metric Spaces into Euclidean Spaces
Published online by Cambridge University Press: 20 November 2018
Extract
In a recent paper on isotopy invariants (1), S. T. Hu denned the enveloping space Em(X) of any given topological space X for each integer m > 1. By an application of the Smith theory to the singular cohomology of the enveloping space Em(X), he obtained his immersion classes 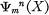 for every n = 1, 2, 3, . . . and proved (3) the main theorem that a necessary condition for a compact metric space X to be immersible into the ^-dimensional Euclidean space Rn is
for every n = 1, 2, 3, . . . and proved (3) the main theorem that a necessary condition for a compact metric space X to be immersible into the ^-dimensional Euclidean space Rn is 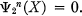 . This theorem was proved earlier by W. T. Wu (4) for finitely triangulable spaces X using purely combinatorial methods.
. This theorem was proved earlier by W. T. Wu (4) for finitely triangulable spaces X using purely combinatorial methods.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1965


