Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Müller, Paul F. X.
and
Schechtman, Gideon
1989.
Geometric Aspects of Functional Analysis.
Vol. 1376,
Issue. ,
p.
113.
Alspach, Dale E.
and
Ullrich, David C.
1989.
Projections onto translation-invariant subspaces of 𝐻¹(𝑅).
Transactions of the American Mathematical Society,
Vol. 313,
Issue. 2,
p.
571.
Alspach, Dale E.
1991.
A characterization of the complemented translation-invariant subspaces of 𝐻¹(𝑅).
Transactions of the American Mathematical Society,
Vol. 323,
Issue. 1,
p.
197.
Kislyakov, S.V.
2001.
Vol. 1,
Issue. ,
p.
871.
Wojtaszczyk, P.
2003.
Vol. 2,
Issue. ,
p.
1671.
Andersson, Mats
2004.
Integrable factors in compact Schur multipliers.
Proceedings of the American Mathematical Society,
Vol. 133,
Issue. 5,
p.
1469.
Rzeszut, Maciej
and
Wojciechowski, Michał
2017.
Independent sums of Hn1(T) and Hn1(δ).
Journal of Functional Analysis,
Vol. 273,
Issue. 2,
p.
836.


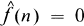 for all integers
for all integers 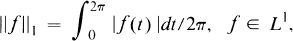
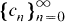 in
in