Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T00:32:41.938Z Has data issue: false hasContentIssue false
  • English
  • Français

Holomorphic Functions with Positive Real Part

Published online by Cambridge University Press:  20 November 2018

Eric Sawyer
Eric Sawyer*
Affiliation:
University of Wisconsin, Madison, Wisconsin
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The main purpose of this note is to prove a special case of the following conjecture.

Conjecture. If F is holomorphic on the unit ball Bn in Cn and has positive real part, then F is in Hp(Bn) for 0 < p < ½(n + 1).

Here Hp(Bn) (0 < p < ∞) denote the usual Hardy spaces of holomorphic functions on Bn. See below for definitions. We remark that the conjecture is known for 0 < p < 1 and that some evidence for it already exists in the literature; for example [1, Theorems 3.11 and 3.15] where it is shown that a particular extreme element of the convex cone of functions

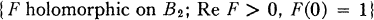
is in Hp(B2) for 0 < p < 3/2.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 34 , Issue 1 , 01 February 1982 , pp. 1 - 7
Copyright
Copyright © Canadian Mathematical Society 1982

References

1. Forelli, F., Measures whose Poisson integrals are pluriharmonic II, Illinois J. Math. 19 (1975), 584–592.Google Scholar
2. Hormander, L., An introduction to complex analysis in several variables (North-Holland, 2nd éd., 1972).Google Scholar
3. Stein, E. M., Boundary behaviour of holomorphic functions of several complex variables (Princeton University Press, 1972.Google Scholar