Given a 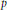$p$-dimensional oriented foliation of an $n$-dimensional compact manifold 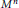${{M}^{n}}$ and a transversal invariant measure $\tau$, Sullivan has defined an element of 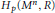${{H}_{p}}\left( {{M}^{n}},\,R \right)$. This generalized the notion of a $\mu$-asymptotic cycle, which was originally defined for actions of the real line on compact spaces preserving an invariant measure $\mu$. In this one-dimensional case there was a natural 1–1 correspondence between transversal invariant measures $\tau$ and invariant measures $\mu$ when one had a smooth flow without stationary points.

For what we call an oriented action of a connected Lie group on a compact manifold we again get in this paper such a correspondence, provided we have what we call a positive quantifier. (In the one-dimensional case such a quantifier is provided by the vector field defining the flow.) Sufficient conditions for the existence of such a quantifier are given, together with some applications.