Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T10:11:12.314Z Has data issue: false hasContentIssue false
  • English
  • Français

Heegner Points over Towers of Kummer Extensions

Published online by Cambridge University Press:  20 November 2018

Henri Darmon  and
Ye Tian
Henri Darmon*
Affiliation:
Department of Mathematics, McGill University, Montréal, PQ H3A 2T5
Ye Tian*
Affiliation:
Academy of Mathematics and System Science, Chinese Academy of Sciences, Beijing100190, P.R.China
*
[email protected]
[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 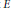$E$ be an elliptic curve, and let 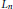${{L}_{n}}$ be the Kummer extension generated by a primitive 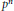${{p}^{n}}$-th root of unity and a 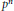${{p}^{n}}$-th root of $a$ for a fixed 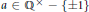$a\,\in \,{{\mathbb{Q}}^{\times }}\,-\,\left\{ \pm 1 \right\}$. A detailed case study by Coates, Fukaya, Kato and Sujatha and $V$. Dokchitser has led these authors to predict unbounded and strikingly regular growth for the rank of 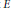$E$ over 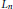${{L}_{n}}$ in certain cases. The aim of this note is to explain how some of these predictions might be accounted for by Heegner points arising from a varying collection of Shimura curve parametrisations.

Keywords

11G0511R2311F46
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 62 , Issue 5 , 01 October 2010 , pp. 1060 - 1081
Copyright
Copyright © Canadian Mathematical Society 2010

References

[BD1] Bertolini, M. and Darmon, H., Kolyvagin's descent and Mordell-Weil groups over ring class fields. J. Reine Angew. Math. 412(1990), 63–74. doi=10.1007/s002220050105Google Scholar
[BD2] Bertolini, M. and Darmon, H., Heegner points on Mumford–Tate curves. Invent. Math. 126(1996), no. 3, 413–456. doi:10.1007/s002220050105Google Scholar
[BD3] Bertolini, M. and Darmon, H., A rigid analytic Gross–Zagier formula and arithmetic applications. Ann. of Math. 146(1997), no. 1, 111–147. doi:10.2307/2951833Google Scholar
[BD4] Bertolini, M. and Darmon, H., Iwasawa's main conjecture for elliptic curves over anticyclotomic Zp-extensions. Ann. of Math. (2) 162(2005), no. 1, 1–64. doi:10.4007/annals.2005.162.1Google Scholar
[CFKS] Coates, J., Fukaya, T., Kato, K., and Sujatha, R., Root numbers, Selmer groups, and non-commutative Iwasawa theory. J. Algebraic Geom. 19(2010), no. 1, 19–97.Google Scholar
[Cole] Coleman, R. F., A p-adic Shimura isomorphism and p-adic periods of modular forms. In: p-adic monodromy and the Birch and Swinnerton-Dyer conjecture (Boston, MA, 1991), Contemp. Math. 165, American Mathematical Society, Providence, RI, 1994, pp. 21–51.Google Scholar
[Cor] Cornut, C., Mazur's conjecture on higher Heegner points. Invent. Math. 148(2002), no. 3, 495–523. doi:10.1007/s002220100199Google Scholar
[Do-TV1] Dokchitser, T. and Dokchitser, V., Computations in Non-commutative Iwasawa theory.With an appendix by J. Coates and R. Sujatha. Proc. London Math. Soc. (3) 94(2007), no. 1, 211–272. doi:10.1112/plms/pdl014Google Scholar
[Do-TV2] Dokchitser, T. and Dokchitser, V., Self-duality of Selmer groups. Math. Proc. Cambridge Philos. Soc. 146(2009), no. 2, 257–267. doi:10.1017/S0305004108001989Google Scholar
[Do-V] Dokchitser, V., Root numbers of non-abelian twists of elliptic curves.With an appendix by Tom Fisher. Proc. London Math. Soc. (3) 91(2005), no. 2, 300–324. doi:10.1112/S0024611505015261Google Scholar
[Gr] Gross, B. H.. Heights and the special values of L-series. In: Number theory, C MS Conf. Proc. 7, American Mathematical Society, Providence, RI, 1987, pp. 115–187.Google Scholar
[Har] Harris, M.. Systematic growth of Mordell-Weil groups of abelian varieties in towers of number fields. Invent. Math. 51(1979), no. 2, 123–141. doi:10.1007/BF01390224Google Scholar
[HV] Hachimori, Y. and Venjakob, O., Completely faithful Selmer groups over Kummer extensions. Kazuya Kato's fiftieth birthday. Doc. Math. 2003, Extra Vol., 443–478.Google Scholar
[Ka] Kato, K., p-adic Hodge theory and values of zeta functions of modular forms. In: Cohomologies p-adiques et applications arithmétiques. III. Astérisque 295(2004), 117–290.Google Scholar
[Ko1] Kolyvagin, V. A., The Mordell–Weil and Shafarevich–Tate groups for Weil elliptic curves. Izv. Akad. Nauk SSSR Ser. Mat. 52(1988), no. 6, 1154–1180, 1327; translation in Math. USSR-Izv. 33(1989), no. 3, 473–499.Google Scholar
[Ko2] Kolyvagin, V. A., Euler systems. In: The Grothendieck Festschrift, Vol. II, Prog. Math., 87, Birkh˜auser, Boston, 1990, pp. 453–483.Google Scholar
[KL] Kolyvagin, V. A. and D. Yu. Logachev, Finiteness ofXover totally real fields. (Russian) Izv. Akad. Nauk SSSR Ser. Mat. 55(1991), no. 4, 851–876; translation in Math. USSR-Izv. 39(1992), no. 1, 829–853.Google Scholar
[Lo] Longo, M., On the Birch and Swinnerton-Dyer conjecture for modular elliptic curves over totally real fields. Ann. Inst. Fourier (Grenoble) 56(2006), no. 3, 689–733.Google Scholar
[Ma] Mazur, B., Rational points of abelian varieties with values in towers of number fields. Invent. Math. 18(1972), 183–266. doi:10.1007/BF01389815Google Scholar
[Mat] Matsuno, K., Finite ¤-submodules of Selmer groups of abelian varieties over cyclotomic Zp-extensions. J. Number Theory 99(2003), no. 2, 415–443. doi:10.1016/S0022-314X(02)00078-1Google Scholar
[Ne1] Nekovar, J., Selmer complexes. Astérisque 310(2006).Google Scholar
[Ne2] Nekovar, J., On the parity of ranks of Selmer groups IV. Compositio Math. 145(2009), no. 6, 1351–1359. doi:10.1112/S0010437X09003959Google Scholar
[Rib] Ribet, K.. Letter to J-F. Mestre. in ar Xiv:math.AG/0105124.Google Scholar
[Ro] Rohrlich, D.E., On L-functions of elliptic curves and cyclotomic towers. Invent. Math. 75(1984), no. 3, 409–423. doi:10.1007/BF01388636Google Scholar
[Sk] Skinner, Christopher, Main conjectures and modular forms, Current Developments in Mathematics 2004(2006), 141–161.Google Scholar
[TZ] Tian, Y. and Zhang, S., Kolyvagin systems of Heegner points on Shimura curves. Forthcoming, Higher Education Press, Beijing, 2011.Google Scholar
[Va1] Vatsal, V., Uniform distribution of Heegner points. Invent. Math. 148(2002), no. 1, 1–46. doi:10.1007/s002220100183Google Scholar
[Va2] Vatsal, V., Special values of anticyclotomic L-functions. Duke Math. J. 116(2003), no. 2, 219–261. doi:10.1215/S0012-7094-03-11622-1Google Scholar
[Zh1] Zhang, S., Height of Heegner points on Shimura curves. Ann. of Math. (2) 153(2001), no. 1, 27–147. doi:10.2307/2661372Google Scholar
[Zh2] Zhang, S., Gross–Zagier formula for GL2. Asian J. Math. 5(2001), no. 2, 183–290.Google Scholar
[Zh3] Zhang, S., Gross–Zagier formula for GL(2). II. In: Heegner points and Rankin L-series, Math. Sci. Res. Inst. Publ. 49, Cambridge Univ. Press, Cambridge, 2004, pp. 191–214.Google Scholar