Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-24T05:28:40.288Z Has data issue: false hasContentIssue false
  • English
  • Français

Heegner Points on Cartan Non-split Curves

Published online by Cambridge University Press:  20 November 2018

Daniel Kohen  and
Ariel Pacetti
Daniel Kohen
Affiliation:
IMAS-CONICET, Buenos Aires, Argentina e-mail: [email protected]
Ariel Pacetti
Affiliation:
Departamento de Matemática, Facultad de Ciencias Exactas y Naturales, Universidad de Buenos Aires and IMAS, CONICET, Argentina e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 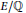$E/\mathbb{Q}$ be an elliptic curve of conductor 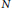$N$ , and let 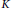$K$ be an imaginary quadratic field such that the root number of 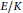$E/K$ is −1. Let 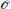$O$ be an order in 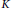$K$ and assume that there exists an odd prime 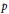$p$ such that 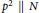${{p}^{2}}\,\parallel \,N$ , and 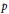$p$ is inert in 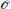$O$ . Although there are no Heegner points on 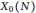${{X}_{0}}(N)$ attached to 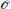$O$ , in this article we construct such points on Cartan non-split curves. In order to do that, we give a method to compute Fourier expansions for forms on Cartan non-split curves, and prove that the constructed points form a Heegner system as in the classical case.

Keywords

11G0511F30Cartan curvesHeegner points
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 68 , Issue 2 , 01 April 2016 , pp. 422 - 444
Copyright
Copyright © Canadian Mathematical Society 2016

References

[AL78] Atkin, A. O. L. and Li, W. C. W., Twists of newforms and pseudo-eigenvalues of W -operators. Invent. Math. 48(1978), no. 3, 221–243.http://dx.doi.Org/10.1007/BF01390245http://dx.doi.org/10.1007/BF01390245Google Scholar
[Che98] Chen, I., The Jacobians of non-split Cartan modular curves. Proc. London Math. Soc. 77(1998), 1–38.http://dx.doi.org/10.1112/S0024611598000392 Google Scholar
[Dar04] Darmon, H., Rational points on modular elliptic curves. CBMS Regional Conference Series in Mathematics, 101, American Mathematical Society, Providence, RI, 2004.Google Scholar
[DD11] Dokchitser, T. and Dokchitser, V., Euler factors determine local Weil representations. arxiv:1112.4889 Google Scholar
[DS05] Diamond, F. and Shurman, J., A first course in modular forms. Graduate Texts in Mathematics, 228, Springer-Verlag, New York, 2005.Google Scholar
[dSE00] de Smit, B. and Edixhoven, B., Sur un résultat d'Imin Chen. Math. Res. Lett. 7(2000), no. 2–3, 147–153. http://dx.doi.org/10.4310/MRL.2000.v7.n2.a1 Google Scholar
[Edi96] Edixhoven, B., On a result oflmin Chen. arxiv:alg-geom/9604008 Google Scholar
[Gro84] Gross, B. H., Heegner points on X0(N). In: Modular forms (Durham, 1983), Ellis Horwood Ser. Math. Appl.: Statist. Oper. Res., Horwood, Chichester, 1984, pp. 87–105.Google Scholar
[Gro91] Gross, B. H., Kolyvagin's work on modular elliptic curves. In: L-functions and arithmetic (Durham, 1989), London Math. Soc. Lecture Note Ser., 153, Cambridge University Press, Cambridge, 1991, pp. 235–256.http://dx.doi.org/10.1017/CBO9780511526053.009 Google Scholar
[GZ86] Gross, B. H. and Zagier, D. B., Heegner points and derivatives of L-series. Invent. Math. 84(1986), no. 2, 225–320. http://dx.doi.org/10.1007/BF01388809 Google Scholar
[Lan87] Lang, S., Elliptic functions. Second ed., Graduate Texts in Mathematics, 112, Springer-Verlag, New York, 1987. http://dx.doi.org/10.1007/978-1-4612-4752-4 Google Scholar
[Maz78] Mazur, B., Rational isogenies of prime degree (with an appendix by D. Goldfeld). Invent. Math. 44(1978), no. 2, 129–162.http://dx.doi.org/10.1007/BF01390348 Google Scholar
[Pacl3] Pacetti, A., On the change of root numbers under twisting and applications. Proc. Amer. Math. Soc. 141(2013), no. 8, 2615–2628.http://dx.doi.Org/10.1090/S0002-9939-2013-11532-7 Google Scholar
[PAR14] PARI Group, Bordeaux. PARI/GP version 2.7.0, 2014. http://pari.math.u-bordeaux.fr/ Google Scholar
[Raj98] Rajan, C. S., On strong multiplicity one for ℓ-adic representations. Internat. Math. Res. Notices 1998, no. 3, 161–172. http://dx.doi.org/10.1155/S1073792898000142 Google Scholar
[RW14] Rebolledo, M. and Wuthrich, C., A moduli interpretation for the non-split Cartan modular curve. http://arxiv:1402.3498 Google Scholar
[Ser67] Serre, J.-P., Complex multiplication. In: Algebraic Number Theory (Proc. Instructional Conf., Brighton, 1965), Thompson, Washington, D.C., 1967, pp. 292–296.Google Scholar
[Ser97] Serre, J.-P., Lectures on the Mordell-Weil theorem. Third ed., Aspects of Mathematics. Friedr. Vieweg & Sohn, Braunschweig, 1997.Google Scholar
[Shi94] Shimura, G., Introduction to the arithmetic theory of automorphic functions. Publications of the Mathematical Society of Japan, 11, Princeton University Press, Princeton, NJ, 1994.Google Scholar
[Zha01] Zhang, S.-W., Gross-Zagier formula for GL2. Asian J. Math. 5(2001), no. 2, 183–290.Google Scholar
[Zha04] Zhang, S.-W., Gross-Zagier formula for GL(2). II. In: Heegner points and Rankin L-series, Math. Sci. Res. Inst. Publ., 49, Cambridge University Press, Cambridge, 2004, pp. 191–214.http://dx.doi.org/10.1017/CBO9780511756375.008 Google Scholar