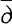Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T00:59:41.505Z Has data issue: false hasContentIssue false
  • English
  • Français

The Heat Equation for the -Neumann Problem, II

Published online by Cambridge University Press:  20 November 2018

Richard Beals  and
Nancy K. Stanton
Richard Beals
Affiliation:
Yale University, New Haven, Connecticut
Nancy K. Stanton
Affiliation:
University of Notre Dame, Notre Dame, Indiana
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Ω be a compact complex n + 1-dimensional Hermitian manifold with smooth boundary M. In [2] we proved the following.

THEOREM 1. Suppose 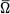satisfies condition Z(q) with 0 ≦ q ≦ n. Let □p,q denote the 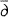-Laplacian on (p, q) forms on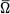which satisfy the 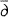-Neumann boundary conditions. Then as t → 0;,

(0.1)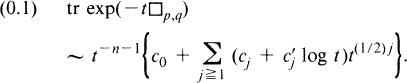

(If q = n + 1, the 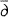-Neumann boundary condition is the Dirichlet boundary condition and the corresponding result is classical.)

Theorem 1 is a version for the 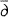-Neumann problem of results initiated by Minakshisundaram and Pleijel [8] for the Laplacian on compact manifolds and extended by McKean and Singer [7] to the Laplacian with Dirichlet or Neumann boundary conditions and by Greiner [5] and Seeley [9] to elliptic boundary value problems on compact manifolds with boundary. McKean and Singer go on to show that the coefficients in the trace expansion are integrals of local geometric invariants.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 40 , Issue 2 , 01 April 1988 , pp. 502 - 512
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Beals, R., Greiner, P. C. and Stanton, N. K., The heat equation on a CR manifold, J. Differential Geometry 20 (1984), 343–387.Google Scholar
2. Beals, R. and Stanton, N. K., The heat equation for the d-Neumann problem, I, Comm. P.D.E. 12 (1987), 351–413.Google Scholar
3. Bedford, E. and Burns, D., Holomorphic mapping of annuli in Cn and the associated extremal function, Annali Scuola Normale Sup. Pisa Série 4, 6 (1979), 381–414.Google Scholar
4. Donnelly, H., Invariance theory of Hermitian manifolds, Proc. A.M.S. 58 (1976), 229–233.Google Scholar
5. Greiner, P. C., An asymptotic expansion for the heat equation, Arch. Rational Mech. Anal. 41 (1971), 163–218.Google Scholar
6. Lempert, L., La métrique de Kobayashi et la représentation des domaines sur la boule, Bull. Soc. Math, de France 109 (1981), 427–474.Google Scholar
7. McKean, H. P. Jr. and Singer, I. M., Curvature and the eigenvalues of the Laplacian, J. Differential Geometry 1 (1967), 43–69.Google Scholar
8. Minakshisundaram, S. and Pleijel, A., Some properties of the eigenfunctions of the Laplace operator on Riemannian manifolds, Can. J. Math. 1 (1949), 242–256.Google Scholar
9. Seeley, R., Analytic extension of the trace associated with elliptic boundary value problems, Amer. J. Math. 91 (1969), 963–983.Google Scholar
10. Stanton, C. M., Intrinsic connections for Levi metrics, in preparation.CrossRefGoogle Scholar
11. Webster, S. M., Pseudo-hermitian structures on a real hypersurface, J. Differential Geometry 13 (1978), 25–41.Google Scholar