Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T02:19:17.403Z Has data issue: false hasContentIssue false
  • English
  • Français

A Hardy-Davies-Petersen Inequality for a Class of Matrices

Published online by Cambridge University Press:  20 November 2018

P. D. Johnson Jr.  and
R. N. Mohapatra
P. D. Johnson Jr.
Affiliation:
American University of Beirut, Beirut, Lebanon
R. N. Mohapatra
Affiliation:
University of Alberta, Edmonton, Alberta
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let ω be the set of all real sequences a = ﹛an﹜n ≧0. Unless otherwise indicated operations on sequences will be coordinatewise. If any component of a has the entry oo the corresponding component of a-1 has entry zero. The convolution of two sequences s and q is given by s * q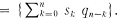. The Toeplitz martix associated with sequence s is the lower triangular matrix 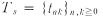defined by tnk = sn-k (n ≧ k), tnk = 0 (n < k). It can be seen that Ts(q) = s * q for each sequence q and that Ts is invertible if and only if s0 ≠ 0. We shall denote a diagonal matrix with diagonal sequence s by Ds.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 30 , Issue 3 , 01 June 1978 , pp. 458 - 465
Copyright
Copyright © Canadian Mathematical Society 1978

References

1. Borwein, D., On products of sequences, J. London Math. Soc. 33 (1958), 212–220.Google Scholar
2. Davies, G. S. and Petersen, G. M., On an inequality of Hardy's (II, Quart. J. Math. (Oxford) (2) 15 (1964), 35–40.Google Scholar
3. Hardy, G. H., Littlewood, J. E. and Pólya, G. , Inequalities (Cambridge, 1934).Google Scholar
4. Johnson, P. D., Jr. and Mohapatra, R. N., The maximal normal subspace of the inverse image of a normal space of sequences by a non-negative matrix transformation, to appear.Google Scholar
5. Johnson, P. D., Jr. and Mohapatra, R. N., Inequalities involving lower-triangular matrices, to appear.Google Scholar
6. Leibowitz, G. M., A note on Cesdro sequence spaces, Tamkang, J. Math. 2 (1971), 151–157.Google Scholar
7. Petersen, G. M., An equality of Hardy's, Quart. J. Math. (Oxford) (2) 15 (1964), 35–40.Google Scholar