Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-17T19:07:09.321Z Has data issue: false hasContentIssue false
  • English
  • Français

Hardy Spaces of Conjugate Systems of Temperatures

Published online by Cambridge University Press:  20 November 2018

Martha Guzmán-Partida  and
Salvador Pérez-Esteva
Martha Guzmán-Partida
Affiliation:
Instituto de Matemáticas Universidad Nacional Autónoma de México Ciudad Universitaria D. F., 04510 México, e-mail: [email protected]
Salvador Pérez-Esteva
Affiliation:
Instituto de Matemáticas Universidad Nacional Autónoma de México Unidad Cuernavaca Apartado Postal 273-3 Administración de correos #3 Cuernavaca, Morelos, 62251 México, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We define Hardy spaces of conjugate systems of temperature functions on 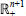$\mathbb{R}_{+}^{n+1}$. We show that their boundary distributions are the same as the boundary distributions of the usual Hardy spaces of conjugate systems of harmonic functions.

Keywords

42B3042A5035K05
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 50 , Issue 3 , 01 June 1998 , pp. 605 - 619
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Baransky, F. and Musialek, J., On the Green functions for the heat equation over the m-dimensional cuboid. Demonstratio Math. (2) XIV (1981), 371–382.Google Scholar
2. Bear, H.S., Hardy spaces of heat functions. Trans. Amer.Math. Soc. (2) 301(1987), 831–844.Google Scholar
3. Cannon, J.R., The One-dimensional Heat Equation. Encyclopedia of Math. and its Appl. 23, Addison- Wesley, 1984.Google Scholar
4. Fefferman, C. and Stein, E.M., Hp spaces of several variables. Acta Math. 129(1972), 137–193.Google Scholar
5. Flett, T.M., Temperatures, Bessel potentials and Lipschitz spaces. Proc. LondonMath. Soc. (3) 22(1971), 385–451.Google Scholar
6. García-Cuerva, J. and Rubio, J.L. de Francia,Weighted norm inequalities and related topics. NotasMat. 116, North Holland, Amsterdam, 1985.Google Scholar
7. Guzmán-Partida, M., Hardy spaces of conjugate temperatures. Studia Math. (2) 122(1997), 153–165.Google Scholar
8. Hirschman, I.I. and Widder, D.V., The Convolution Transform. Princeton Univ. Press, 1955.Google Scholar
9. Kochneff, E. and Sagher, Y., Conjugate Temperatures. J. Approx. Theory (1) 70(1992), 39–49.Google Scholar
10. Pérez-Esteva, S.,Hardy spaces of vector-valued heat functions. Houston J.Math. (1) 19(1993), 127–134.Google Scholar
11. Riesz, M., L’integrale de Riemann-Liouville et le problem de Cauchy. Acta Math. 81(1949), 1–223. 12. Stein, E.M., Harmonic Analysis. Real-variableMethods,Orthogonality and Oscillatory Integrals. Princeton Univ. Press, 1993.Google Scholar
13. Stein, E.M. and Weiss, G., On the theory of harmonic functions of several variables. I. The theory of Hp spaces. Acta Math. 103(1960), 25–62.Google Scholar