Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T00:47:26.921Z Has data issue: false hasContentIssue false
  • English
  • Français

Haar Null Sets and the Consistent Reflection of Non-meagreness

Published online by Cambridge University Press:  20 November 2018

Márton Elekes  and
Juris Steprāns
Márton Elekes
Affiliation:
Rényi Alfréd Institute, Reáltanoda u. 13-15, Budapest 1053, Hungary Institute of Mathematics, Eötvös Loránd University, Pázmány Péter s. 1/c, Budapest 1117, Hungary e-mail: [email protected]
Juris Steprāns
Affiliation:
Department of Mathematics, York University, TorontoON M3J 1P3. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A subset 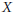$X$ of a Polish group 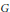$G$ is called Haar null if there exist a Borel set 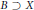$B\,\supset \,X$ and Borel probability measure 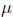$\mu$ on 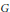$G$ such that 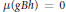$\mu \left( g\,Bh \right)\,=\,0$ for every 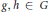$g,\,h\,\in \,G$. We prove that there exist a set 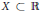$X\,\subset \,\text{R}$ that is not Lebesgue null and a Borel probability measure 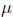$\mu$ such that 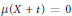$\mu \left( X\,+\,t \right)\,=\,0$ for every 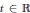$t\,\in \,\text{R}$. This answers a question from David Fremlin’s problem list by showing that one cannot simplify the definition of a Haar null set by leaving out the Borel set $B$. (The answer was already known assuming the Continuum Hypothesis.)

This result motivates the following Baire category analogue. It is consistent with 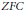$ZFC$ that there exist an abelian Polish group 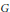$G$ and a Cantor set 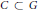$C\,\subset \,G$ such that for every non-meagre set 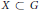$X\,\subset \,\text{G}$ there exists a 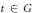$t\in \text{G}$ such that $C\,\cap \,\left( X\,+\,t \right)$ is relatively non-meagre in $C$. This essentially generalizes results of Bartoszyński and Burke–Miller.

Keywords

28C1003E3503E1722C0528A78Haar nullChristensennon-locally compact Polish grouppacking dimensionProblem FC on Fremlin's listforcinggeneric real
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 66 , Issue 2 , 01 April 2014 , pp. 303 - 322
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Bartoszyński, T., On perfectly meager sets. Proc. Amer. Math. Soc. 130(2002), no. 4, 1189–1195. http://dx.doi.org/10.1090/S0002-9939-01-06138-X Google Scholar
[2] Bartoszyński, T. and Judah, H., Set theory. On the structure of the real line. A. K. Peters,Wellesley, MA, 1995.Google Scholar
[3] Burke, M. R. and Miller, A.W., Models in which every nonmeager set is nonmeager in a nowhere dense Cantor set. Canad. J. Math. 57(2005), no. 6, 1139–1154. http://dx.doi.org/10.4153/CJM-2005-044-x Google Scholar
[4] Christensen, J. P. R., On sets of Haar measure zero in abelian Polish groups. Proceedings of the International Symposium on Partial Differential Equations and the Geometry of Normed Linear Spaces (Jerusalem, 1972). Israel J. Math. 13(1972), 255–260. http://dx.doi.org/10.1007/BF02762799 Google Scholar
[5] Christensen, J. P. R., Measure theoretic zero sets in infinite dimensional spaces and applications to differentiability of Lipschitz mappings. Actes du Deuxième Colloque d’Analyse Fonctionnelle de Bordeaux (Univ.Bordeaux, 1973). Publ. Dép. Math. (Lyon) 10(1973), no. 2, 29–39.Google Scholar
[6] Ciesielski, K. and Shelah, S., Category analogue of sup-measurability problem. J. Appl. Anal. 6(2000), no. 2, 159–172.Google Scholar
[7] Darji, U. B. and Keleti, T., Covering R with translates of a compact set. Proc. Amer. Math. Soc. 131(2003), no. 8, 2593–2596.Google Scholar
[8] Dougherty, R. and Mycielski, J., The prevalence of permutations with infinite cycles. Fund. Math. 144(1994), no. 1, 89–94.Google Scholar
[9] Erdőos, P. and Kakutani, S., On a perfect set. Colloquium Math. 4(1957), 195–196.Google Scholar
[10] Falconer, K. J., The geometry of fractal sets. Cambridge Tracts in Mathematics, 85, Cambridge University Press, Cambridge, 1986.Google Scholar
[11] Hunt, B. R., The prevalence of continuous nowhere differentiable functions. Proc. Amer. Math. Soc. 122(1994), no. 3, 711–717. http://dx.doi.org/10.1090/S0002-9939-1994-1260170-X Google Scholar
[12] Hunt, B. R., Sauer, T., and Yorke, J. A., Prevalence: a translation-invariant “almost every” on infinite-dimensional spaces. Bull. Amer. Math. Soc. (N.S.) 27(1992), no. 2, 217–238. http://dx.doi.org/10.1090/S0273-0979-1992-00328-2 Google Scholar
[13] A. S. Kechris, , Classical descriptive set theory. Graduate Texts in Mathematics, 156, Springer-Verlag, 1995.Google Scholar
[14] Mattila, P., Geometry of sets and measures in Euclidean spaces. Fractals and rectifiability. Cambridge Studies in Advanced Mathematics, 44, Cambridge University Press, Cambridge, 1995.Google Scholar
[15] A. Rosłanowski, and Shelah, S., Measured creatures. Israel J. Math. 151(2006), 61–110. http://dx.doi.org/10.1007/BF02777356 Google Scholar
[16] Zajíček, L., On differentiability properties of typical continuous functions and Haar null sets. Proc. Amer. Math. Soc. 134(2006), no. 4, 1143–1151. http://dx.doi.org/10.1090/S0002-9939-05-08203-1 Google Scholar