Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T01:03:17.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Growth Conditions and Decomposable Operators

Published online by Cambridge University Press:  20 November 2018

Mehdi Radjabalipour
Mehdi Radjabalipour*
Affiliation:
University of Toronto, Toronto, Ontario; Dalhousie University, Halifax, Nova Scotia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Throughout this paper T will denote a bounded linear operator which is defined on a Banach space 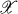and whose spectrum lies on a rectifiable Jordan curve J .

The operators having some growth conditions on their resolvents have been the subject of discussion for a long time. Many sufficient conditions have been found to ensure that such operators have invariant subspaces [2 ; 3 ; 7 ; 8 ; 12 ; 13; 14; 21; 27; 28; 29], are S-operators [14], are quasidecomposable [9], are decomposable [4 ; 11], are spectral [7 ; 10 ; 15 ; 17], are similar to normal operators [16 ; 23 ; 25 ; 26], or are normal [15 ; 18 ; 22]. In this line we are going to show that many such operators are decomposable.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 26 , Issue 6 , December 1974 , pp. 1372 - 1379
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Apostol, C., Spectral decomposition and functional calculus, Rev. Roumaine Math. Pures Appl. 13 (1968), 1481–1528.Google Scholar
2. Apostol, C., On the growth of resolvent, perturbation and invariant subspaces, Rev. Roumaine Math. Pures Appl. 16 (1971), 161–172.Google Scholar
3. Bartle, R. G., Spectral localization of operators in Banach space, Math. Ann. 153 (1964), 261–269.Google Scholar
4. Colojoara, I. and Foias, C., The theory of generalized spectral operators (Gordon Breachr Science Publ., New York, 1968).Google Scholar
5. Colojoara, I. and Foias, C., Quasi-nilpotent equivalence of not necessarily commuting operators, J. Math. Mech. 15 (1965), 521–540.Google Scholar
6. Davis, Ch., Spectrum of an operator and of its restriction, Revised form 1972 (unpublished manuscript).Google Scholar
7. Dunford, N. and Schwartz, J., Linear operators. Ill (Interscience, New York, 1971).Google Scholar
8. Godement, R., Théorème Taubériene et théorie spectrals, Ann. Sci. Ecole Norm. Sup. 64 (1947), 119–138.Google Scholar
9. Jafarian, A. A., Spectral decomposition of operators on Banach spaces, Ph.D. Thesis, University of Toronto, 1973.Google Scholar
10. Jafarian, A. A., On reductive operators, Indiana Univ. Math. J. (to appear).Google Scholar
11. Jafarian, A. A., Some results on -unitary, -self adjoint and decomposable operators, Indiana Univ. Math. J. (to appear).Google Scholar
12. Kitano, K., Invariant subspaces of some non-self adjoint operators, Tôhoku Math. J. 20 (1968), 313–322.Google Scholar
13. Leaf, G. K., A spectral theory for a class of linear operators, Pacific J. Math. 13 (1963), 141–155.Google Scholar
14. Ljubic, J. I. and Macaev, V. I., Operators with separable spectrum, Trans. Amer. Math. Soc. 47 (1965), 89–129.Google Scholar
15. Nordgren, E., Radjavi, H., and Rosenthal, P., On operators with reducing invariant subspaces, Amer. J. Math, (to appear).Google Scholar
16. Radjabalipour, M., Some results on power bounded operators, Indiana Univ. Math. J. 22 (1973), 673–677.Google Scholar
17. Radjabalipour, M., Growth conditions, spectral operators and reductive operators (to appear).Google Scholar
18. Radjabalipour, M., On normality of operators, Indiana Univ. Math. J. (to appear).Google Scholar
19. Radjabalipour, M., Operators with growth conditions, Ph.D. Thesis, University of Toronto, 1973.Google Scholar
20. Radjavi, H. and Rosenthal, P., Invariant subspaces (Springer Verlog, Berlin, 1973).Google Scholar
21. Schwartz, J., Subdiagonalization of operators in Hilbert space with compact imaginary part, Comm. Pure. Appl. Math. 15 (1962), 159–172.Google Scholar
22. Stampfli, J. G., A local spectral theory for operators, J. Functional Analysis 4 (1969), 1–10.Google Scholar
23. Stampfli, J. G., A local spectral theory for operators, III, Resolvents, spectral sets and similarity, Trans. Amer. Math. Soc. 168 (1972), 133–151.Google Scholar
24. Stampfli, J. G., A local spectral theory for operators, IV; Invariant subspaces, Indiana Univ. Math. J. 22 (1972), 159–167.Google Scholar
25. Sz-Nagy, B., On uniformly bounded linear transformations in Hilbert space, Acta. Sci. Math. (Szeged) 11 (1947), 152–157.Google Scholar
26. Sz-Nagy, B. and Foias, C., Harmonic analysis of operators on Hilbert space (North-Holland, Amsterdam, 1970).Google Scholar
27. Tillmann, H. G., Eine erweiterung des funktionalkalkùls fur lineare operatoren, Math. Ann. 151 (1963), 424–430.Google Scholar
28. Wermer, J., The existence of invariant subspaces, Duke Math. J. 19 (1952), 615–622.Google Scholar
29. Wolf, F., Operators in Banach space which admit a generalized spectral decomposition, Nederl. Akad. Wetensch. Proc. Ser A éo = Indag. Math. 19 (1957), 302–311.Google Scholar