The aim of the present paper is the computation of Green's functions for the powers 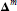${{\mathbf{\Delta }}^{m}}$ of the invariant Laplace operator on rank-one Hermitian symmetric spaces. Starting with the noncompact case, the unit ball in 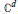${{\mathbb{C}}^{d}}$, we obtain a complete result for 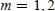$m\,=\,1,\,2$ in all dimensions. For 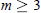$m\,\ge \,3$ the formulas grow quite complicated so we restrict ourselves to the case of the unit disc 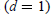$(d\,=\,1)$ where we develop a method, possibly applicable also in other situations, for reducing the number of integrations by half, and use it to give a description of the boundary behaviour of these Green functions and to obtain their (multi-valued) analytic continuation to the entire complex plane. Next we discuss the type of special functions that turn up (hyperlogarithms of Kummer). Finally we treat also the compact case of the complex projective space 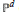${{\mathbb{P}}^{d}}$ (for 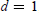$d\,=\,1$, the Riemann sphere) and, as an application of our results, use eigenfunction expansions to obtain some new identities involving sums of Legendre 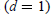$(d\,=\,1)$ or Jacobi 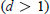$(d\,>\,1)$ polynomials and the polylogarithm function. The case of Green's functions of powers of weighted (no longer invariant, but only covariant) Laplacians is also briefly discussed.