Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T00:40:56.608Z Has data issue: false hasContentIssue false
  • English
  • Français

Green's Forms and Meromorphic Functions on Compact Analytic Varieties

Published online by Cambridge University Press:  20 November 2018

Kunihiko Kodaira
Kunihiko Kodaira*
Affiliation:
Institute for Advanced Study, PrincetonN.J.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 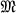be a compact complex analytic variety of the complex dimension n with a positive definite Kâhlerian metric [4] ; the local analytic coordinates on 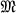will be denoted by z = (z1z2, … , zn). Now, suppose a meromorphic function f(z) defined on 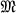as given. Then the poles and zero-points of f(z) constitute an analytic surface in 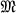consisting of a finite number of irreducible closed analytic surfaces Γ1, Γ2, … , Γk, each of which is a polar or a zero-point variety of f(z).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 3 , 1951 , pp. 108 - 128
Copyright
Copyright © Canadian Mathematical Society 1951

References

[1] Bochner, S. and Martin, W. T., Several complex variables (Princeton, 1948).Google Scholar
[2] F., Hartogs, Über die aus den singulären Stellen einer analytischen Funktion mehreren Veränderlichen bestehenden Gebilde, Acta Math., vol. 32 (1909), 57–79.Google Scholar
[3] Hodge, W. V. D., The theory and applications of harmonic integrals (Cambridge Univ.Press, 1941).Google Scholar
[4] Kähler, E., Über eine bemerkenswerte Hermitische Metrik,Abh. Math. Sem. Hamburg, vol. 9 (1933), 173–186.Google Scholar
[5] Kodaira, K., Harmonic fields in Riemannian manifolds, Annals of Math., vol. 50 (1949), 587–665.Google Scholar
[6] Kodaira, K., Qn the existence of analytic functions on closed analytic surfaces, Kodai Math. Sem. Reports, vol. 1 (1949), 21–26.Google Scholar
[7] Koopman, B. O. and Brown, A. B., On the covering of analytic loci by complexes, Trans. Amer. Math. Soc., vol. 34 (1932), 231–251.Google Scholar
[8] Lefschetz, S., Topology, Amer. Math. Soc. Colloq. Publ., vol. XII (1930).Google Scholar
[9] Lefschetz, S., and Whitehead, J. H. C, On analytic complexes, Trans. Amer. Math. Soc, vol. 35 (1933), 510–517.Google Scholar
[10] G., de Rham, Sur la théorie des formes différentielles harmoniques, Ann. Univ. Grenobles, vol. 22 (1946), 135–152.Google Scholar
[11] van der Waerden, B. L., Topologische Begründung des Kalküls der abzählenden Geometrie, Math. Ann., vol. 102 (1929), 337–362.Google Scholar
[12] Weil, A., Sur la théorie des formes différentielles attachées à une variété analytique complexe, Comm. Math. Helv., vol. 20 (1947), 110–116.Google Scholar
[13] Weyl, H., Die Idee der Riemannschen Fläche (Berlin, 1913).Google Scholar
[14] Weyl, H., Method of orthogonal projection in potential theory, Duke Math. J., vol. 7 (1940), 411–444.Google Scholar
[15] Weyl, H., On Hodge's Theory of harmonie integrals, Annals of Math., vol. 44 (1943), pp. 1–6.Google Scholar