Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-28T17:12:17.474Z Has data issue: false hasContentIssue false
  • English
  • Français

Green Function and Self-adjoint Laplacians on Polyhedral Surfaces

Part of: Deformations of analytic structures Partial differential equations on manifolds; differential operators Riemann surfaces Spectral theory and eigenvalue problems

Published online by Cambridge University Press:  02 July 2019

Alexey Kokotov  and
Kelvin Lagota
Alexey Kokotov
Affiliation:
Department of Mathematics and Statistics, Concordia University, 1455 de Maisonneuve Blvd. West, Montreal, Québec, H3G 1M8 Email: [email protected]@concordia.ca
Kelvin Lagota
Affiliation:
Department of Mathematics and Statistics, Concordia University, 1455 de Maisonneuve Blvd. West, Montreal, Québec, H3G 1M8 Email: [email protected]@concordia.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

Using Roelcke’s formula for the Green function, we explicitly construct a basis in the kernel of the adjoint Laplacian on a compact polyhedral surface 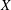$X$ and compute the 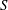$S$-matrix of 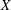$X$ at the zero value of the spectral parameter. We apply these results to study various self-adjoint extensions of a symmetric Laplacian on a compact polyhedral surface of genus two with a single conical point. It turns out that the behaviour of the 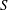$S$-matrix at the zero value of the spectral parameter is sensitive to the geometry of the polyhedron.

Keywords

self-adjoint extensionLaplacianpolyhedral surface

MSC classification

Primary: 30F30: Differentials on Riemann surfaces
Secondary: 30F45: Conformal metrics (hyperbolic, Poincaré, distance functions) 35P99: None of the above, but in this section 58J52: Determinants and determinant bundles, analytic torsion 30F10: Compact Riemann surfaces and uniformization 32G15: Moduli of Riemann surfaces, Teichmüller theory
Type
Article
Information
Canadian Journal of Mathematics , Volume 72 , Issue 5 , October 2020 , pp. 1324 - 1351
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aissiou, T., Hillairet, L., and Kokotov, A., Determinants of pseudo-laplacians. Math. Res. Lett. 19(2012), no. 6, 1297–1308. https://doi.org/10.4310/MRL.2012.v19.n6.a10CrossRefGoogle Scholar
Akhiezer, N. I. and Glazman, I. M., Theory of linear operators in Hilbert space. (vol. 1–2, Monographs and Studies in Mathematics, 9. Pitman (Advanced Publishing Program), Boston, Mass.-London, 1981.Google Scholar
Albeverio, S., Gesztesy, F., Hoegh-Krohn, R., and Holden, H., Solvable models in quantum mechanics. Second ed., AMS Chelsea Publishing, Providence, RI, 2005.Google Scholar
Berezin, F. and Shubin, M., The Schrödinger equation. In: Mathematics and its Applications (Soviet Series), 66. Kluwer Academic Publishers, 1991. https://doi.org/10.1007/978-94-011-3154-4Google Scholar
Colin De Verdiere, Y., Pseudo-laplaciens. I. Ann. Inst. Fourier 32(1982), 275–286.CrossRefGoogle Scholar
Farkas, H. and Kra, I., Riemann surfaces. In: Graduate Texts in Mathematics, 71. Springer-Verlag, New York-Berlin, 1980.Google Scholar
Fay, J., Theta functions on Riemann surfaces. In: Lecture notes in Mathematics, 352. Springer-Verlag, Berlin-New York, 1973.Google Scholar
Fay, J., Kernel functions, analytic torsion and moduli spaces. Mem. Amer. Math. Soc. 96(1992), no. 464. https://doi.org/10.1090/memo/0464Google Scholar
Hillairet, L., Spectral theory of translation surfaces: a short introduction. In: Actes du Séminaire de Théorie Spectrale et Géometrie, 28. Année 2009-2010, Sémin. Théor. Spectr. Géom., 28, Univ. Grenoble I, Saint-Martin-d’Hères, 2010, pp. 51–62.https://doi.org/10.5802/tsg.278Google Scholar
Hillairet, L. and Kokotov, A., Krein formula and S-matrix for Euclidean surfaces with conical singularities. J. Geom. Anal. 23(2013), no. 3, 1498–1529. https://doi.org/10.1007/s12220-012-9295-3CrossRefGoogle Scholar
Hillairet, L. and Kokotov, A., Isospectrality, comparison formulas for determinants of Laplacian and flat metrics with non-trivial holonomy. Proc. Amer. Math. Soc. 145(2017), 3915–3928. https://doi.org/10.1090/proc/13494CrossRefGoogle Scholar
Hillairet, L., Kalvin, V., and Kokotov, A., Moduli spaces of meromorphic functions and determinant of Laplacian. Trans. Amer. Math. Soc. 370(2018), 4559–4599. https://doi.org/10.1090/tran/7430CrossRefGoogle Scholar
Kay, B. S. and Studer, U. M., Boundary conditions for quantum mechanics on cones and fields around cosmic strings. Comm. Math. Phys. 139(1991), 103–139.CrossRefGoogle Scholar
Kirsten, K., Loya, P., and Park, J., Functional determinants for general self-adjoint extensions of Laplace type operators resulting from the generalized cone. Manuscripta Math. 125(2008), 95–126. https://doi.org/10.1007/s00229-007-0142-yCrossRefGoogle Scholar
Kokotov, A., Polyhedral surfaces and determinant of Laplacian. Proc. Amer. Math. Soc. 141(2013), 725–735. https://doi.org/10.1090/S0002-9939-2012-11531-XCrossRefGoogle Scholar
Kokotov, A. and Korotkin, D., Tau-functions on spaces of Abelian differentials and higher genus generalization of Ray-Singer formula. J. Differential Geom. 82(2009), no. 1, 35–100.CrossRefGoogle Scholar
Kondratjev, V. A., Boundary value problems for elliptic equations in domains with conical and angle points. Proc. Moscow Math. Soc. 16(1967), 209–292.Google Scholar
Lebedev, N. N., Special functions and their applications. In: Dover Books on Mathematics. reprint of 1965 ed.Google Scholar
Loya, P., McDonald, P., and Park, J., Zeta regularized determinants for conic manifolds. J. Funct. Anal. 242(2007), 195–229. https://doi.org/10.1016/j.jfa.2006.04.014CrossRefGoogle Scholar
Lukzen, E. N. and Shafarevich, A. I., On the kernel of the Laplace operator on two-dimensional polyhedra. Russ. J. Math. Phys. 24(2017), 508–514. https://doi.org/10.1134/S1061920817040070CrossRefGoogle Scholar
Maz’ya, V., Nazarov, S., and Plamenevskij, B., Asymptotic theory of elliptic boundary value problems in singularly perturbed domains. In: Operator Theory: Advances and Applications, 112. Birkhäuser Verlag, Basel, 2000.Google Scholar
Maz’ya, V. and Plamenevskij, B., Asymptotic behavior of the fundamental solutions of elliptic boundary value problems in domains with conical points. In: Probl. Mat. Anal., 7. Leningrad. Univ., Leningrad, 1979, pp. 100–145.Google Scholar
McMullen, C. T., Billiards and Teichmuller curves on Hiilbert modular surfaces. J. Amer. Math. Soc. 16(2003), 857–885. https://doi.org/10.1090/S0894-0347-03-00432-6CrossRefGoogle Scholar
Mooers, E. A., Heat kernel asymptotics on manifolds with conic singularities. J. Anal. Math. 78(1999), 1–36. https://doi.org/10.1007/BF02791127CrossRefGoogle Scholar
Nazarov, S. and Plamenevsky, B., Elliptic problems in domains with piecewise smooth boundaries. In: de Gruyter Expositions in Mathematics, 13. de Gruyter, Berlin, 1994. https://doi.org/10.1515/9783110848915.525Google Scholar
Okikiolu, K., Extremals for logarithmic Hardy-Littlewood-Sobolev inequalities on compact manifolds. Geom. Funct. Anal. 17(2008), 1655–1684. https://doi.org/10.1007/s00039-007-0636-5CrossRefGoogle Scholar
Polyakov, A. M., Quantum geometry of bosonic strings. Phys. Lett. B 103(1981), 207–210. https://doi.org/10.1016/0370-2693(81)90743-7CrossRefGoogle Scholar
Reed, M. and Simon, B., Methods of modern mathematical physics. II. In: Fourier analysis, self-adjointness. Academic Press/Harcourt Brace, New York-London, 1975.Google Scholar
Schiffer, M. and Spencer, D., Functionals of finite Riemann surfaces. Princeton University Press, Princeton, NJ, 1954.Google Scholar
Steiner, J., A geometrical mass and its extremal properties for metrics on S 2. Duke Math. J. 129(2005), 63–86. https://doi.org/10.1215/S0012-7094-04-12913-6CrossRefGoogle Scholar
Taylor, M. E., Partial differential equations. I. In: Basic Theory. Springer, New York, 1999.Google Scholar
Troyanov, M., Les surfaces euclidiennes à singularités coniques. Enseign. Math. 32(1968), 79–94.Google Scholar
Tyurin, A. N., Periods of quadratic differentials. Russian Math. Surveys 33(1978), 149–195, 272.CrossRefGoogle Scholar
Verlinde, E. and Verlinde, H., Chiral bosonization, determinants and the string partition function. Nuclear Phys. B 288(1987), 357–396. https://doi.org/10.1016/0550-3213(87)90219-7CrossRefGoogle Scholar