Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T02:39:03.685Z Has data issue: false hasContentIssue false
  • English
  • Français

Gosset Polytopes in Picard Groups of del Pezzo Surfaces

Published online by Cambridge University Press:  20 November 2018

Jae-Hyouk Lee
Jae-Hyouk Lee*
Affiliation:
Korea Institute for Advanced Study, KIAS Hoegiro 87(207-43 Cheongnyangni-dong), Dongdaemun-gu, Seoul 130-722, Korea and Department ofMathematics, EwhaWomans University, 11-1 Daehyun-dong, Seodaenum-gu, Seoul 120-750, Korea email: [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this article, we study the correspondence between the geometry of del Pezzo surfaces 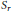${{s}_{r}}$ and the geometry of the $r$-dimensional Gosset polytopes (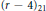${{(r-4)}_{21}}$. We construct Gosset polytopes 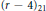${{(r-4)}_{21}}$ in Pic 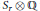${{S}_{r}}\,\otimes \,\mathbb{Q}$ whose vertices are lines, and we identify divisor classes in Pic 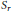${{s}_{r}}$ corresponding to 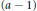$(a-1)$-simplexes 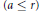$(a\le r)$, 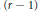$(r-1)$-simplexes and 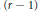$(r-1)$-crosspolytopes of the polytope 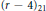${{(r-4)}_{21}}$. Then we explain how these classes correspond to skew $a$-lines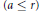$(a\le r)$, exceptional systems, and rulings, respectively.

As an application, we work on the monoidal transform for lines to study the local geometry of the polytope 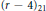${{(r-4)}_{21}}$. And we show that the Gieser transformation and the Bertini transformation induce a symmetry of polytopes 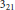${{3}_{21}}$ and 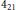${{4}_{21}}$, respectively.

Keywords

51M2014J2622E99
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 64 , Issue 1 , 01 February 2012 , pp. 123 - 150
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Batyrev, V. V. and Popov, O. N., The Cox ring of a del Pezzo surface. In: Arithmetic of Higher-Dimensional Algebraic Varieties. Progr. Math. 226. Birkhäuser Boston, Boston, Ma, 2004, pp. 85-103.Google Scholar
[2] Buckley, A. and Košir, T., Determinantal representations of smooth cubic surfaces. Geom. Dedicata 125(2007), no. 1, 115-140. http://dx. doi. org/10.1007/s10711-007-9144-xGoogle Scholar
[3] Conway, J. H. and Sloane, N. J. A., Sphere Packings, Lattices and Groups. Third edition. Grundlehren der Mathematischen. Wissenschaften 290. Springer-Verlag, New York, 1999.Google Scholar
[4] Coxeter, H. S. M., The polytope 221, whose twenty-seven vertices correspond to the lines on the general cubic surface. Amer. J. Math. 62(1940), 457-486. http://dx. doi. org/10.2307/2371466Google Scholar
[5] Coxeter, H. S. M., Regular and semiregular polytopes. II. Math. Z. 188(1985), no. 4, 559-591. http://dx. doi. org/10.1007/BF01161657Google Scholar
[6] Coxeter, H. S. M., Regular and semi-regular polytopes. III. Math. Z. 200(1988), no. 1, 3-45. http://dx. doi. org/10.1007/BF01161745Google Scholar
[7] Coxeter, H. S. M., The evolution of Coxeter-Dynkin diagrams. Nieuw Arch. Wisk. 9(1991), no. 3, 233-248.Google Scholar
[8] Coxeter, H. S. M., Regular Complex Polytopes. Second edition. Cambridge University Press, Cambridge, 1991.Google Scholar
[9] Demazure, M., Surfaces de del Pezzo I, II, III, IV, V. In: Séminaire sur les singularités des surfaces, Lecture Notes in Mathematics, 777, Springer-Verlag, Berlin-Heidelberg-New York, 1980, pp. 21-69. http://dx. doi. org/10.1007/BFb0085872Google Scholar
[10] Dolgachev, I. V.. Topics in Classical Algebraic Geometry. Part I (2009), http://www. math. lsa. umich. edu/_idolga/lecturenotes. html.Google Scholar
[11] Du Val, P.. On the directrices of a set of points in a plane. Proc. London Math. Soc. 35(1933), no. 2, 23-74. http://dx. doi. org/10.1112/plms/s2-35.1.23Google Scholar
[12] Friedman, R. and Morgan, J., Exceptional groups and del Pezzo surfaces. In: Symposium in Honor of C. H. Clemens. Contemp. Math. 312. American Mathematical Society, Providence, RI, 2002, pp. 101-116.Google Scholar
[13] Hartshorne, R., Algebraic Geometry. Graduate Texts in Mathematics 52. Springer-Verlag, New York, 1977.Google Scholar
[14] Lee, J. H., Configuration of lines in del Pezzo surfaces with Gosset polytopes. arxiv:1001.4174Google Scholar
[15] Leung, N. C., ADE-bundles over rational surfaces, configuration of lines and rulings. arxiv:math/0009192Google Scholar
[16] Leung, N. C. and Zhang, J. J.. Moduli of bundles over rational surfaces and elliptic curves I. Simply laced cases. http://www. ims. cuhk. edu. hk/_leung/ConanPaper/ConanPaper. html.Google Scholar
[17] Manin, Y., Cubic Forms: Algebra, Geometry, Arithmetic. Second edition. English translation, North-Holland Mathematical Library 4. North-Holland, Amsterdam, 1986.Google Scholar
[18] Manivel, L., Configurations of lines and models of Lie algebras. J. Algebra 304(2006), no. 1, 457-486. http://dx. doi. org/10.1016/j. jalgebra.2006.04.029Google Scholar