Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T14:05:16.319Z Has data issue: false hasContentIssue false
  • English
  • Français

Global Well-Posedness and Convergence Results for the 3D-Regularized Boussinesq System

Published online by Cambridge University Press:  20 November 2018

Ridha Selmi
Ridha Selmi*
Affiliation:
Mathematics Department, Faculty of Sciences of Gabés, University of Gabés, Cité Erriadh, 6072 Zrig, Gabés, Tunisia and PDEs and Applications Lab, Faculty of Sciences of Tunis, University of Tunis El Manar, Campus Universitaire, 2092 El Manar, Tunis, Tunisia email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

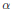Analytical study of the regularization of the Boussinesq system is performed in frequency space using Fourier theory. Existence and uniqueness of weak solutions with minimum regularity requirement are proved. Convergence results of the unique weak solution of the regularized Boussinesq system to a weak Leray–Hopf solution of the Boussinesq system are established as the regularizing parameter $\alpha$ vanishes. The proofs are done in the frequency space and use energy methods, the Arselà-Ascoli compactness theorem and a Friedrichs-like approximation scheme.

Keywords

35A0576D0335B4035B1086A0586A10regularizing Boussinesq systemexistence and uniqueness of weak solutionconvergence resultscompactness method in frequency space
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 64 , Issue 6 , 01 December 2012 , pp. 1415 - 1435
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Benameur, J. and Selmi, R., Study of anisotropic MHD system in anisotropic Sobolev spaces. Ann. Fac. Sci. Toulouse Math. 17(2008), 1–22. http://dx.doi.org/10.5802/afst.1172 Google Scholar
[2] Benameur, J. and Selmi, R., Anisotropic rotating MHD system in critical anisotropic spaces. Mem. Differential Equations Math. Phys. 44(2008), 23–44.Google Scholar
[3] Benameur, J. and Selmi, R., Long-time behavior of periodic Navier–Stokes equations in critical spaces. In: Progress in Analysis and its Applications, World Scientific Publishing Co., Nackensack, NJ, 2010, 597–603.Google Scholar
[4] Benameur, J. and Selmi, R., Long-time decay to the Leray solution of the two-dimensional Navier–Stokes equation. Bull. Lond. Math. Soc., to appear.Google Scholar
[5] Brandolese, L. and Schonbek, M. E., Large time decay and growth for solutions of a viscous Boussinesq system. Trans. Amer. Math. Soc., to appear.Google Scholar
[6] Cao, Y., Lunasin, E. M., and Titi, E. S., Global well-posedness of three-dimensional viscous and inviscid simplified Bardina turbulence models. Comm. Math. Sci. 4(2006), 823–884.Google Scholar
[7] Cao, Y. and Titi, E. S., On the rate of convergence of the two-dimensional C-models of turbulence to the Navier–Stokes equations. Numer. Funct. Anal. Optim. 30(2009), 1231–1271. http://dx.doi.org/10.1080/01630560903439189 Google Scholar
[8] Ebrahimi, M., Holst, M., and Lunasin, E., The Navier–Stokes Voight for image inpainting. Cited on 15 Dec 2009. arxiv:www.ar Xiv:math.NA/0901.4548/Google Scholar
[9] Khouider, B. and Titi, E. S., An inviscid regularization for the surface quasi-geostrophic equation. Comm. Pure Appl. Math. 61(2008), 1331–1346. http://dx.doi.org/10.1002/cpa.20218 Google Scholar
[10] Ladyzhenskaya, O. A., The Boundary Value Problems of Mathematical Physics. Appl. Math. Sci. 49, Springer-Verlag, New York, 1985.Google Scholar
[11] Ladyzhenskaya, O. A., New equations for the description of motion of viscous incompressible fluids and solvability in the large of boundary value problems for them. Proc. Steklov Inst. Math. 102(1967), 95–118.Google Scholar
[12] Linshiz, J. and Titi, E. S., Analytical study of certain magnetohydrodynamics-*-models. J. Math. Phys. 48(2007), 065504. http://dx.doi.org/10.1063/1.2360145 Google Scholar
[13] Lions, J. L., Quelques résultats d’existence dans des équations aux dérivées partielles non linéaires. Bull. Soc. Math. France 87(1959), 245–273.Google Scholar
[14] Pedlosky, J., Geophysical fluid dynamics. Springer-Verlag, New York, 1987.Google Scholar
[15] Rudin, W., Functional Analysis. Second edition, Mc Graw-Hill, Boston, 1991.Google Scholar
[16] Salmon, R., Lectures on geophysical fluid dynamics. Oxford University Press, New York, 1998.Google Scholar
[17] Schwartz, L., Topologie générale et analyse fonctionnelle. Hermann, Paris, 1980.Google Scholar
[18] Selmi, R., Convergence results for MHD system. Int. J. Math. Math. Sci. 2006, Art. ID 28704.Google Scholar
[19] Selmi, R., Asymptotic study of anisotropic periodic rotating MHD system. In: Further Progress in Analysis, World Scientific Publishing Co., Hackensack, NJ, 2009, 368–377.Google Scholar
[20] Selmi, R., Asymptotic study of mixed rotating MHD system. Bull. Korean Math. Soc. 47(2010), 231–249. http://dx.doi.org/10.4134/BKMS.2010.47.2.231 Google Scholar
[21] Smagorinsky, J., General circulation experiments with the primitive equations I. The basic experiment. Monthly Weather Rev. 91(1963), 99–164.Google Scholar
[22] Temam, R., Navier–Stokes equations. Theory and numerical analysis. Third edition. Stud. Math. Appl. 2, North-Holland Publishing Co., Amsterdam, 1984.Google Scholar