Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T00:50:32.032Z Has data issue: false hasContentIssue false
  • English
  • Français

Global Positive Solutions of Semilinear Elliptic Equations

Published online by Cambridge University Press:  20 November 2018

Ezzat S. Noussair  and
Charles A. Swanson
Ezzat S. Noussair
Affiliation:
University of New South Wales, Kensington, Australia
Charles A. Swanson
Affiliation:
University of British Columbia, Vancouver, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The semilinear elliptic boundary value problem

1.1

will be considered in an exterior domain Ω ⊂ Rn, n ≥ 2, with boundary ∂Ω ∊ C2 + α, 0 < α < 1, where

1.2

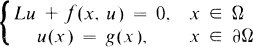
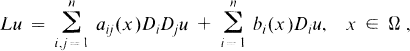
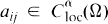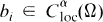Di = ∂/∂xi, i = 1, …, n. The coefficients aij, bi in (1.2) are assumed to be real-valued functions defined in Ω ∪ ∂Ω such that each , , and (aij(x)) is uniformly positive definite in every bounded domain in Ω. The Hölder exponent α is understood to be fixed throughout, 0 < α < 1 . The regularity hypotheses on f and g are stated as H 1 near the beginning of Section 2.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 35 , Issue 5 , 01 October 1983 , pp. 839 - 861
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. Amann., H. Existence and multiplicity theorems for semi-linear elliptic boundary value problems. Math. Z. 750 (1976), 281–295.Google Scholar
2. Krein, M. G. and Rutman, M. A., Linear operators leaving invariant a cone in a Banach space. Amer. Math. Soc. Transi., Ser. 1(10) (1962), 1–128.Google Scholar
3. Ladyzhenskaya, O. A. and Ural'tseva, N. N., Linear and quasilinear elliptic equations (Academic Press, New York, 1968).Google Scholar
4. Nehari, Z., On a class of nonlinear second-order differential equations, Trans. Amer. Math. Soc. 95 (1960), 101–123.Google Scholar
5. Noussair, E. S., On semilinear elliptic boundary value problems in unbounded domains, J. Differential Equations 41 (1981), 334–348.Google Scholar
6. Noussair, E. S. and Swanson, C. A., Positive solutions of semilinear Schrôdinger equations in exterior domains, Indiana Univ. Math. J. 28 (1979), 993–1003.Google Scholar
7. Swanson, C. A., Semilinear second order elliptic oscillation, Can. Math. Bull. 22 (1979), 139–157.Google Scholar