No CrossRef data available.
Published online by Cambridge University Press: 13 September 2022
In this paper, we considered the global strong solution to the 3D incompressible micropolar equations with fractional partial dissipation. Whether or not the classical solution to the 3D Navier–Stokes equations can develop finite-time singularity remains an outstanding open problem, so does the same issue on the 3D incompressible micropolar equations. We establish the global-in-time existence and uniqueness strong solutions to the 3D incompressible micropolar equations with fractional partial velocity dissipation and microrotation diffusion with the initial data 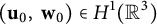 $(\mathbf {u}_0,\ \mathbf {w}_0)\in H^1(\mathbb {R}^3)$.
$(\mathbf {u}_0,\ \mathbf {w}_0)\in H^1(\mathbb {R}^3)$.
Liu is supported by the Panzhihua University Foundation (Grant No. 035200075).