Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Koldobsky, A.
König, H.
and
Zymonopoulou, M.
2008.
The complex Busemann–Petty problem on sections of convex bodies.
Advances in Mathematics,
Vol. 218,
Issue. 2,
p.
352.
Haberl, Christoph
2008.
Lp intersection bodies.
Advances in Mathematics,
Vol. 217,
Issue. 6,
p.
2599.
Yaskin, Vladyslav
2008.
Modified Shephard’s problem on projections of convex bodies.
Israel Journal of Mathematics,
Vol. 168,
Issue. 1,
p.
221.
Li, Lei
and
Ren, Wei Yun
2010.
Isometries on the quasi-Banach spaces L p (0 < p < 1).
Acta Mathematica Sinica, English Series,
Vol. 26,
Issue. 8,
p.
1519.
Koldobsky, Alexander
2011.
Positive definite functions and stable random vectors.
Israel Journal of Mathematics,
Vol. 185,
Issue. 1,
p.
277.
Kalton, N.J.
and
Zymonopoulou, M.
2011.
Positive definite distributions and normed spaces.
Advances in Mathematics,
Vol. 227,
Issue. 2,
p.
986.
Böröczky, Károly J.
Lutwak, Erwin
Yang, Deane
and
Zhang, Gaoyong
2012.
The log-Brunn–Minkowski inequality.
Advances in Mathematics,
Vol. 231,
Issue. 3-4,
p.
1974.
Liu, Qixia
and
Leng, Gangsong
2013.
Volume inequalities for
L
0
-Minkowski combination of convex bodies.
Journal of Inequalities and Applications,
Vol. 2013,
Issue. 1,
Ma, Tongyi
and
Zhang, Lili
2014.
Quasi-Shephard’s problem on projections of convex bodies.
Wuhan University Journal of Natural Sciences,
Vol. 19,
Issue. 1,
p.
55.
Godefroy, G.
2014.
Obituary: Nigel John Kalton, 1946–2010.
Bulletin of the London Mathematical Society,
Vol. 46,
Issue. 6,
p.
1292.
Framstad, Nils Chr.
2015.
Portfolio Theory forα-Symmetric and Pseudoisotropic Distributions:k-Fund Separation and the CAPM.
Journal of Probability and Statistics,
Vol. 2015,
Issue. ,
p.
1.
Koldobsky, Alexander
Merkurjev, Alexander S.
and
Yaskin, Vladyslav
2017.
On polynomially integrable convex bodies.
Advances in Mathematics,
Vol. 320,
Issue. ,
p.
876.
Spencer, Patrick
2017.
Separation inequalities for Lp-centroid bodies.
Indagationes Mathematicae,
Vol. 28,
Issue. 6,
p.
1165.
Naor, Assaf
and
Oleszkiewicz, Krzysztof
2020.
Geometric Aspects of Functional Analysis.
Vol. 2266,
Issue. ,
p.
229.
Wu, Denghui
and
Bu, Zhen-Hui
2022.
The measure-comparison problem for polar (p,μ)-centroid bodies.
Advances in Applied Mathematics,
Vol. 137,
Issue. ,
p.
102332.
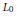 ${{L}_{0}}$
${{L}_{0}}$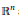 ${{\mathbb{R}}^{n}}$ and construct new bodies using three operations — linear transformations, closure in the radial metric, and multiplicative summation defined by
${{\mathbb{R}}^{n}}$ and construct new bodies using three operations — linear transformations, closure in the radial metric, and multiplicative summation defined by  ${{\left\| x \right\|}_{K+0L}}\,=\,\sqrt{{{\left\| x \right\|}_{K}}{{\left\| x \right\|}_{L}}}$. We prove that in dimension 3 this procedure gives all origin-symmetric convex bodies, while this is no longer true in dimensions 4 and higher. We introduce the concept of embedding of a normed space in
${{\left\| x \right\|}_{K+0L}}\,=\,\sqrt{{{\left\| x \right\|}_{K}}{{\left\| x \right\|}_{L}}}$. We prove that in dimension 3 this procedure gives all origin-symmetric convex bodies, while this is no longer true in dimensions 4 and higher. We introduce the concept of embedding of a normed space in 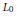 ${{L}_{0}}$ that naturally extends the corresponding properties of
${{L}_{0}}$ that naturally extends the corresponding properties of 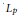 ${{L}_{P}}$-spaces with
${{L}_{P}}$-spaces with 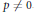 $p\,\ne \,0$, and show that the procedure described above gives exactly the unit balls of subspaces of
$p\,\ne \,0$, and show that the procedure described above gives exactly the unit balls of subspaces of 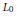 ${{L}_{0}}$ in every dimension. We provide Fourier analytic and geometric characterizations of spaces embedding in
${{L}_{0}}$ in every dimension. We provide Fourier analytic and geometric characterizations of spaces embedding in 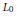 ${{L}_{0}}$, and prove several facts confirming the place of
${{L}_{0}}$, and prove several facts confirming the place of 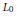 ${{L}_{0}}$ in the scale of
${{L}_{0}}$ in the scale of 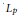 ${{L}_{P}}$-spaces.
${{L}_{P}}$-spaces.