Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T16:53:59.218Z Has data issue: false hasContentIssue false
  • English
  • Français

The Geometry and Fundamental Group of Permutation Products and Fat Diagonals

Published online by Cambridge University Press:  20 November 2018

Sadok Kallel  and
Walid Taamallah
Sadok Kallel
Affiliation:
Laboratoire Painlevé, Université des Sciences et Technologies de Lille, France, and American University of Sharjah, UAE, e-mail: [email protected]
Walid Taamallah
Affiliation:
Facultédes Sciences de Tunis, Department of Mathematics, University of Tunis, El Manar, Tunisia, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Permutation products and their various “fat diagonal” subspaces are studied from the topological and geometric points of view. We describe in detail the stabilizer and orbit stratifications related to the permutation action, producing a sharp upper bound for its depth and then paying particular attention to the geometry of the diagonal stratum. We exhibit an expression for the fundamental group of any permutation product of a connected space 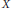$X$ having the homotopy type of a CW complex in terms of 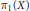${{\pi }_{1}}(X)$ and 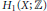${{H}_{1}}(X;\,\mathbb{Z})$. 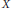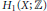We then prove that the fundamental group of the configuration space of $n$-points on $X$, of which multiplicities do not exceed $n/2$, coincides with ${{H}_{1}}(X;\,\mathbb{Z})$. Further results consist in giving conditions for when fat diagonal subspaces of manifolds can be manifolds again. Various examples and homological calculations are included.

Keywords

14F3557F80symmetric productsfundamental grouporbit stratification
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 65 , Issue 3 , 01 June 2013 , pp. 575 - 599
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Adem, A., Duman, A. N., and Gómez, J. M., Cohomology of toroidal orbifold quotients. J. Algebra 344(2011), 114–136. http://dx.doi.org/10.1016/j.jalgebra.2011.08.004 Google Scholar
[2] Aguilar, M. A. and Prieto, C., Transfers for ramified covering maps in homology and cohomology. Int. J. Math. Math. Sci. 2006, Art. ID 94651.Google Scholar
[3] Beshears, A., G-isovariant structure sets and stratified structure sets. Ph.D. Thesis, Vanderbilt University, Proquest LLC, Ann Arbor, MI, 1997.Google Scholar
[4] Birkenhake, C. and Lange, H., A family of abelian surfaces and curves of genus four. Manuscripta Math. 85(1994), no. 3–4, 393–407. http://dx.doi.org/10.1007/BF02568206 Google Scholar
[5] Björner, A. and Welker, V., The homology of “k-equal” manifolds and relation partition lattices. Adv. Math. 110(1995), no. 2, 277–313. http://dx.doi.org/10.1006/aima.1995.1012 Google Scholar
[6] Brown, R. and Higgins, P., The fundamental groupoid of the quotient of a Hausdorff space by a discontinuous action of a discrete group is the orbit groupoid of the induced action. arxiv:math/0212271. Google Scholar
[7] Cameron, P. J., Solomon, R., and Turull, A., Chains of subgroups in symmetric groups. J. Algebra 127(1989), no. 2, 340–352. http://dx.doi.org/10.1016/0021-8693(89)90256-1 Google Scholar
[8] Dimca, A. and Rosian, R., The Samuel stratification of the discriminant is Whitney regular. Geom. Dedicata 17(1984), no. 2, 181–184.Google Scholar
[9] Dold, A., Homology of symmetric products and other functors of complexes. Ann. of Math. (2) 68(1958), 54–80. http://dx.doi.org/10.2307/1970043 Google Scholar
[10] Dold, A. and Puppe, D., Homologie nicht-additiver Funktoren. Anwendungen. Ann. Inst. Fourier Grenoble 11(1961), 201–312. http://dx.doi.org/10.5802/aif.114 Google Scholar
[11] Félix, Y. and Tanré, D., Rational homotopy of symmetric products and spaces of finite subsets. In: Homotopy theory of function spaces and related topics, Contemp. Math., 519, American Mathematical Society, Providence, RI, 2010, pp. 77–92.Google Scholar
[12] Grothendieck, A., Revêtements étales et groupe fondamental. Séminaire de Géométrie Algébrique du Bois Marie 1960–1961 (SGA1). Lecture Notes in Mathematics, 224, Springer-Verlag, Berlin-Heidelberg-New York, 1971.Google Scholar
[13] Hatcher, A., Algebraic topology. Cambridge University Press, Cambridge, 2002.Google Scholar
[14] Hughes, B., Geometric topology of stratified spaces. Electron. Res. Announc. Amer. Math. Soc. 2 2(1996), no. 1, 73–81. http://dx.doi.org/10.1090/S1079-6762-96-00010-8 Google Scholar
[15] Isaacs, I. M., Finite group theory. Graduate Studies in Mathematis, 92, American Mathematical Society, 2008.Google Scholar
[16] Kallel, S., Symmetric products, duality and homological dimension of configuration spaces. In: Groups, homotopy and configuration spaces, Geometry and Topology Monographs, 13, Geom. Topol. Publ., Coventry, 2008, pp. 499–527.Google Scholar
[17] Kallel, S. and Sjerve, D., Remarks on finite subset spaces. Homology, Homotopy Appl. 11(2009), no. 2, 229–250.Google Scholar
[18] Liao, S. D., On the topology of cyclic products of spheres. Trans. Amer. Math. Soc 77(1954), 520–551. http://dx.doi.org/10.1090/S0002-9947-1954-0065924-2 Google Scholar
[19] MacDonald, I. G., The Poincaré polynomial of a symmetric product. Proc. Cambridge Philos. Soc. 58(1962), 563–568. http://dx.doi.org/10.1017/S0305004100040573 Google Scholar
[20] Montgomery, D. and Yang, C. T., The existence of a slice. Ann. of Math 65(1957), 108–116. http://dx.doi.org/10.2307/1969667 Google Scholar
[21] Morton, H. R., Symmetric products of the circle. Proc. Cambridge Philos. Soc. 63(1967), 349–352. http://dx.doi.org/10.1017/S0305004100041256 Google Scholar
[22] Pflaum, M., Analytic and geometric study of stratified spaces. Lecture Notes in Mathematics, 1768, Springer-Verlag, Berlin, 2001.Google Scholar
[23] Smith, P. A., Manifolds with abelian fundamental groups. Ann. of Math. 37(1936), no. 3, 526–533. http://dx.doi.org/10.2307/1968475 Google Scholar
[24] Taamallah, W., Permutation products, configuration spaces with bounded multiplicity and finite subset spaces. Ph.D Thesis, University of Tunis, 2011.Google Scholar
[25] C. H.Wagner, Symmetric, cyclic and permutation products of manifolds. Dissertationes Math. (Rozprawy Mat.), 182(1980).Google Scholar