Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-20T17:29:02.340Z Has data issue: false hasContentIssue false
  • English
  • Français

Geometric and Topological Properties of Certain w* Compact Convex sets which Arise from the Study of Invariant Means

Published online by Cambridge University Press:  20 November 2018

Edmond E. Granirer
Edmond E. Granirer*
Affiliation:
University of British Columbia, Vancouver, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let E be a Banach space, A a subset of its dual E*.x0 ∊ A is said to be a w*Gδ point of A if there are xn ∊ E and scalars γn, n = 1,2, 3 … such that

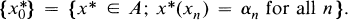
Denote by w*Gδ{A} the set of all w*Gδ points of A. If S is a semigroup of maps on E* and K ⊂ E*, denote by

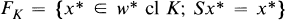
i.e., the set of points x* in the w*closure of K which are fixed points of S (i.e., sx* = x* for each s in S}. An operator will mean a bounded linear map on a Banach space and Co B will denote the convex hull of B ⊂ E.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 37 , Issue 1 , 01 February 1985 , pp. 107 - 121
Copyright
Copyright © Canadian Mathematical Society 1985

References

1. Day, M. M., Amenable semigroups, Illinois J. Math. (1957), 509–544.Google Scholar
2. Diestel, J. and Uhl, J. J., Vector measures, Math Surveys of the AMS 75 (1977).CrossRefGoogle Scholar
3. Ghoussoub, N. and Saab, E., On the weak Radon Nikodym property, Proc. AMS. 81 (1981), 81–84.Google Scholar
4. Granirer, E. E., Exposed points of convex sets and weak sequential convergence, Memoir of the AMS. 123 (1972).Google Scholar
5. Granirer, E. E., Extremely amenable semigroups I(II), Math. Scand. 17 (1965), 177–197 (120 (1967) 93–113).Google Scholar
6. Granirer, E. E., Geometric and topological properties of certain w*-compact convex subsets of double duals of Banach spaces, which arise from the study of invariant means, to appear in Illinois J. Math.Google Scholar
7. Holmes, R. B., A geometric characterisation of non atomic measure spaces, Math. Ann. 182 (1969), 55–59.Google Scholar
8. Lindenstrauss, J., Weakly compact sets, their topological properties and Banach spaces they generate, Proc. Symp. Infinite dimensional topology (1967). Ann. of Math Studies 69 (1972), 235–273, Princeton.Google Scholar
9. Losert, V. and Rindler, H., Almost invariant sets, Bull. London Math. Soc. 13 (1981), 145–148.Google Scholar
10. Phelps, R. R., Dentability and extreme points in Banach spaces, J. Funct. Anal. 16 (1974), 78–90.Google Scholar
11.Rainwater Seminar, Lecture notes 1977.Google Scholar
12. Rosenblatt, J., Uniqueness of invariant means for measure preserving transformations, Trans AMS 265 (1981), 623–636.Google Scholar
13. Rudin, W., Real and complex analysis (McGraw-Hill, 1974).Google Scholar
14. Saab, E., Some characterisations of weak Radon Nikodym sets, Proc. AMS 86 (1982), 307–311.Google Scholar
15. Schaefer, H. H., Banach lattices and positive operators (Springer-Verlag, 1974).CrossRefGoogle Scholar
16. Segal, I., Equivalences of measures spaces, Amer. J. Math. 73 (1951), 275–313.Google Scholar
17. Stegall, C., The Radon-Nikodym property in conjugate Banach spaces II, Trans AMS 264 (1981), 507–519.Google Scholar