Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-26T15:29:48.075Z Has data issue: false hasContentIssue false
  • English
  • Français

Genericity of Representations of p-Adic Sp2n and Local Langlands Parameters

Published online by Cambridge University Press:  20 November 2018

Baiying Liu
Baiying Liu*
Affiliation:
School of Mathematics, University of Minnesota, Minneapolis, MN, U.S.A. email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 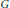$G$ be the $F$-rational points of the symplectic group 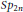$S{{p}_{2n}}$, where $F$ is a non-Archimedean local field of characteristic 0. Cogdell, Kim, Piatetski-Shapiro, and Shahidi constructed local Langlands functorial lifting from irreducible generic representations of 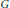$G$ to irreducible representations of 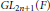$G{{L}_{2n+1}}\left( F \right)$. Jiang and Soudry constructed the descent map from irreducible supercuspidal representations of 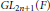$G{{L}_{2n+1}}\left( F \right)$ to those of 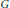$G$, showing that the local Langlands functorial lifting from the irreducible supercuspidal generic representations is surjective. In this paper, based on above results, using the same descent method of studying 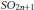$S{{O}_{2n+1}}$ as Jiang and Soudry, we will show the rest of local Langlands functorial lifting is also surjective, and for any local Langlands parameter 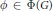$\phi \,\in \,\Phi \left( G \right)$, we construct a representation $\sigma $ such that $\phi $ and $\sigma $ have the same twisted local factors. As one application, we prove the 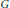$G$-case of a conjecture of Gross-Prasad and Rallis, that is, a local Langlands parameter 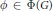$\phi \,\in \,\Phi \left( G \right)$ is generic, i.e., the representation attached to $\phi $ is generic, if and only if the adjoint $L$-function of $\phi $ is holomorphic at 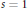$s\,=\,1$. As another application, we prove for each Arthur parameter 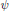$\psi $, and the corresponding local Langlands parameter 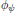${{\phi }_{\psi }}$, the representation attached to 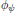${{\phi }_{\psi }}$ is generic if and only if 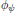${{\phi }_{\psi }}$ is tempered.

Keywords

22E5011S37generic representationslocal Langlands parameters
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 63 , Issue 5 , 18 October 2011 , pp. 1107 - 1136
Copyright
Copyright © Canadian Mathematical Society 2011

References

[A] Arthur, J., Unipotent automorphic representations: conjectures. Orbites et représentations. II. ´ Asterisque, 171–172(1989), 13–71.Google Scholar
[Aub] Aubert, A.-M., Dualité dans le groupe de Grothendieck de la catégorie des représentations lisses de longueur finie d’un groupe réductif p-adique. Trans. Amer. Math. Soc. 347(1995), no. 6, 2179–2189. doi:10.2307/2154931Google Scholar
[Ban1] Ban, D., The Aubert involution and R-groups. Ann. Sci. École Norm. Sup. (4) 35(2002), no. 5, 673–693.Google Scholar
[Ban2] Ban, D., Symmetry of Arthur parameters under Aubert involution. J. Lie Theory 16(2006), no. 2, 251–270.Google Scholar
[BZh] Ban, D. and Y. L. Zhang, Arthur R-groups, classical R-groups, and Aubert involutions for SO(2n + 1). Compos. Math. 141(2005), no. 2, 323–343. doi:10.1112/S0010437X04001113Google Scholar
[B] Borel, A., Automorphic L-functions. In: Automorphic forms, representations and L-functions, (Proc. Sympos. Pure Math., Oregon State Univ., Corvallis, Ore., 1977), Part 2, 2, XXXIII, American Mathematical Society, Providence, RI, 1979, pp. 27–61.Google Scholar
[BZ] Bernstein, I. N. and A. V. Zelevinsky, Induced representations of reductive p-adic groups. I. Ann. Sci. École Norm. Sup. 10(1977), no. 4, 441–472.Google Scholar
[C] Casselman, W., Introduction to the theory of admissible representations of p-adic reductive groups. Preprint, http://www.math.ubc.ca/ ∼ cass/research.htmlGoogle Scholar
[CKP-SS] Cogdell, J. W., H. H. Kim, I. I. Piatetski-Shapiro, and F. Shahidi, Functoriality for the classical groups. Publ. Math. Inst. Hautes Études Sci. 99(2004), 163–233.Google Scholar
[FH] Fulton, W. and J. Harris, Representation theory. A first course. Graduate Texts in Mathematics, 129, Springer-Verlag, New York, 1991.Google Scholar
[GP] Gross, B. H. and D. Prasad, On the decomposition of a representation of SO when restricted to SO n−1 . Canad. J. Math. 44(1992), no. 5, 974–1002. doi:10.4153/CJM-1992-060-8Google Scholar
[GR] Gross, B. and M. Reeder, Arithmetic invariants of discrete Langlands parameters. Duke Math. J. 154(2010), no. 3, 431–508. doi:10.1215/00127094-2010-043 nGoogle Scholar
[HT] Harris, M. and R. Taylor, The geometry and cohomology of some simple Shimura varieties. Annals of Mathematics Studies, 151, Princeton University Press, Princeton, NJ, 2001.Google Scholar
[H1] Henniart, G., Une preuve simple des conjectures de Langlands pour GL(n) sur un corps p-adique. Invent. Math. 139(2000), no. 2, 439–455. doi:10.1007/s002220050012Google Scholar
[H2] Henniart, G., Correspondance de Langlands et fonctions L des carrés extérieur et symétrique. Int. Math. Res. Not. IMRN 2010, no. 4, 633–673.Google Scholar
[Hb] Herb, R. A., Elliptic representations of Sp(2n) and SO(n). Pacific J. Math. 161(1993), no. 2, 347–358.Google Scholar
[JP-SS] Jacquet, H., I. I. Piatetski-Shapiro, and J. A. Shalika, Rankin–Selberg convolutions. Amer. J. Math. 105(1983), no. 2, 367–464. doi:10.2307/2374264Google Scholar
[Jan] Jantzen, C., On square-integrable representations of classical p-adic groups. II. Represent. Theory 4(2000), 127–180. doi:10.1090/S1088-4165-00-00081-9Google Scholar
[Jng] Jiang, D., On local γ-factors. In: Arithmetic geometry and number theory, Series on Number Theory and Applications, 1, World Sci. Publ., Hackensack, NJ, 2006, pp. 1–28.Google Scholar
[JngS1] Jiang, D. and D. Soudry, The local converse theorem for SO(2n + 1) and applications. Ann. of Math. 157(2003), no. 3, 743–806. doi:10.4007/annals.2003.157.743Google Scholar
[JngS2] Jiang, D. and D. Soudry, Generic representations and the local Langlands reciprocity law for p-adic SO(2n + 1). In: Contributions to automorphic forms, geometry, and number theory, Johns Hopkins Univ. Press, Baltimore, MD, 2004, pp. 457–519.Google Scholar
[JngS3] Jiang, D. and D. Soudry, On local descent from GL(n) to classical groups. Preprint, dhjiang/Papers/papers.html.Google Scholar
[Kn] Knapp, A. W., Introduction to the Langlands program. In: Representation theory and http://www.math.umn.edu/ ∼ automorphic forms (Edinburgh, 1996), Proc. Sympos. Pure Math., 61, American Mathematical Society, Providence, RI, 1997, pp. 245–302.Google Scholar
[Ku] Kudla, S., The local Langlands correspondence: the non-Archimedean case. In: Motives (Seattle, WA, 1991), Proc. Sympos. Pure Math., 55, Part 2, American Mathematical Society, Providence, RI, 1994, pp. 365–391.Google Scholar
[Liu] Liu, B. Y., Generic representations and local Langlands reciprocity law for p-adic symplectic groups. (Chinese), Master’s thesis, Harbin Insitute of Technology, 2008.Google Scholar
[M1] Mui, G.ć, Some results on square integrable representations; irreducibility of standard representations. Internat. Math. Res. Notices 1998, no. 14, 705–726.Google Scholar
[M2] Mui, G.ć, On generic irreducible representations of Sp(n, F) and SO(2n + 1, F). Glas. Mat. Ser. III 33(53)(1998), no. 1, 19–31.Google Scholar
[Rod] Rodier, F., Whittaker models for admissible representations of reductive p-adic split groups. In: Harmonic analysis on homogeneous spaces (Proc. Sympos. Pure Math., Vol. XXVI, Williams Coll., Williamstown, Mass., 1972), American Mathematical Society, Providence, RI, 1973, pp. 425–430.Google Scholar
[S1] Shahidi, F., A proof of Langlands’ conjecture on Plancherel measures; complementary series for p-adic groups. Ann. of Math. 132(1990), no. 2, 273–330. doi:10.2307/1971524Google Scholar
[S2] Shahidi, F., On multiplicativity of local factors. In: Festchrift in honor of I. I. Piatetski-Shapiro on the occasion of his sixtieth birthday, Part II, Israel Math. Conf. Proc., 3, Weizmann, Jerusalem, 1990, pp. 279–289.Google Scholar
[Td] Tadi, M.ć, On regular square integrable representations of classical p-adic groups. Amer. J. Math. 120(1998), no. 1, 159–210. doi:10.1353/ajm.1998.0007Google Scholar
[T] Tate, J.. Number theoretic background. In: Automorphic forms, representations and L-functions (Proc. Sympos. Math., Oregon State Univ., Corvallis, Ore., 1977), Part 2, Proc. Sympos. Pure Math., XXXIII, American Mathematical Society, Providence, RI, 1979, pp. 3–26.Google Scholar
[Z] Zelevinsky, A. V., Induced representations of reductive p-adic groups. II. On irreducible representations of GL(n). Ann. Sci. École. Norm. Sup. 13(1980), no. 2, 165–210.Google Scholar