Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-13T08:19:21.793Z Has data issue: false hasContentIssue false
  • English
  • Français

Generic Extensions and Canonical Bases for Cyclic Quivers

Published online by Cambridge University Press:  20 November 2018

Bangming Deng ,
Jie Du  and
Jie Xiao
Bangming Deng
Affiliation:
School of Mathematical Sciences, Beijing Normal University, Beijing 100875, P.R. China email: [email protected]
Jie Du
Affiliation:
School of Mathematics and Statistics, University of New South Wales, Sydney, NSW 2052, Australia email: [email protected]
Jie Xiao
Affiliation:
Department of Mathematical Sciences, Tsinghua University, Beijing 100084, P.R. China email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We use the monomial basis theory developed by Deng and Du to present an elementary algebraic construction of the canonical bases for both the Ringel–Hall algebra of a cyclic quiver and the positive part 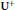${{\mathbf{U}}^{+}}$ of the quantum affine 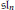$\mathfrak{s}{{\mathfrak{l}}_{n}}$. This construction relies on analysis of quiver representations and the introduction of a new integral PBW-like basis for the Lusztig 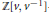$\mathbb{Z}[v,\,{{v}^{-1}}]$-form of 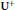${{\mathbf{U}}^{+}}$.

Keywords

17B3716G20
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 59 , Issue 6 , 01 December 2007 , pp. 1260 - 1283
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Beck, J., Chari, V. and Pressley, A., An algebraic characterization of the affine canonical basis. Duke Math. J. 99(1999), no. 3, 455–487.Google Scholar
[2] Beck, J. and Nakajima, H., Crystal bases and two sided cells of quantum affine algebras. Duke Math. J. 123(2004), no. 2, 335–402.Google Scholar
[3] Bongartz, K., On degenerations and extensions of finite-dimensional modules. Adv. Math. 121(1996), no. 2, 245–287.Google Scholar
[4] Deng, B. and Du, J., Monomial bases for quantum affin. Adv. Math. 191(2005), no. 2, 276–304.Google Scholar
[5] Deng, B. and Du, J., bases of quantized enveloping algebras. Pacific J. Math. 220(2005), no. 1, 33–48.Google Scholar
[6] Deng, B. and Du, J., Frobenius morphisms and representations of algebras. Trans. Amer. Math. Soc. 358(2006), no. 8, 3591–3622.Google Scholar
[7] Dlab, V. and Ringel, C. M., On algebras of finite representation type. J. Algebra 33(1975), 306–394.Google Scholar
[8] Dlab, V. and Ringel, C. M., Indecomposable representations of graphs and algebras. Memoirs Amer. Math. Soc. 6(1976), no. 173.Google Scholar
[9] Du, J., A matrix approach to IC bases. In: Representations of Algebras, CMS Conf. Proc. 14, American Mathematical Society, Providence, RI, 1993, pp. 165–174.Google Scholar
[10] Du, J., IC bases and quantum linear groups. In: Algebraic Groups and Their Generalizations: Quantum and Infinite-DimensionalMethods, Proc. Sympos. Pure Math. 56, American Mathematical Society, Providence, RI, 1994, pp. 135–148.Google Scholar
[11] Du, J. and Parshall, B., Monomial bases for q-Schur algebras. Trans. Amer. Math. Soc. 355(2003), no. 4, 1593–1620.Google Scholar
[12] Grojnowski, I. and Lusztig, G., A comparison of bases of quantized enveloping algebras. In: Linear Algebraic Groups and Their Representations, Contemp. Math. 153, American Mathematical Society, Providence, RI, 1993, 11–19.Google Scholar
[13] Guo, J. Y., The Hall polynomials of a cyclic serial algebra. Comm. Algebra 23(1995), no. 2, 743–751.Google Scholar
[14] Kashiwara, M., On cystal bases of the Q-analogue of universal enveloping algebras. Duke Math. J. 63(1991), no. 2, 465–516.Google Scholar
[15] Kazhdan, D. and Lusztig, G., Representations of Coxeter groups and Hecke algebras. Invent. Math. 53(1979), no. 2, 165–184.Google Scholar
[16] Leclerc, B., Thibon, J.-Y., and Vasserot, E., Zelevinsky's involution at roots of unity. J. Reine Angew. Math. 513(1999), 33–51.Google Scholar
[17] Lin, Z., Xiao, J. and Zhang, G., Representations of tame quivers and affine canonical bases. arXiv:0706.1444v3.Google Scholar
[18] Lusztig, G., Canonical bases arising from quantized enveloping algebras, J. Amer.Math. Soc. 3(1990), no. 2, 447–498.Google Scholar
[19] Lusztig, G., Quivers, perverse sheaves, and quantized enveloping algebras. J. Amer. Math. Soc. 4(1991), 365–421.Google Scholar
[20] Lusztig, G., Affine quivers and canonical bases. Inst. Hautes Études Sci. Publ. Math. 76(1992), 111–163.Google Scholar
[21] Lusztig, G., Introduction to Quantum Groups, Progress in Mathematics 110, Birkhäuser Boston, Boston MA, 1993.Google Scholar
[22] Mah, A., Generic extension monoids for cyclic quivers. Ph. D. thesis, University of New South Wales, Sydney, 2006.Google Scholar
[23] Moody, R. V. and Pianzola, A., Lie algebras with triangular decompositions. John Wiley and Sons, New York 1995.Google Scholar
[24] Reineke, M., Generic extensions and multiplicative bases of quantum groups at q = 0. Represent. Theory 5(2001), 147–163 (electronic).Google Scholar
[25] Ringel, C. M., Hall algebras and quantum groups. Invent. Math. 101(1990), no. 3, 583–591.Google Scholar
[26] Ringel, C. M., The composition algebra of a cyclic quiver. Proc. London Math. Soc. 66(1993), no. 3, 507–537.Google Scholar
[27] Ringel, C. M., Hall algebras revisited. In: Quantum Deformations of Algebras and Their Representations. Israel Math. Conf. Proc. 7, Bar-Ilan Univ., Ramat Gan, 1993, pp. 171–176.Google Scholar
[28] Ringel, C. M., The Hall algebra approach to quantum groups. In: XI Latin American School of Mathematics (Spanish). Aportaciones Mat. Comun. 15, Soc. Mat. Mexicana, Mexico, 1995. pp. 85–114.Google Scholar
[29] Schiffmann, O., The Hall algebra of a cyclic quiver and canonical bases of Fock spaces. Internat. Math. Res. Notices (2000), no. 8, 413–440.Google Scholar
[30] Varagnolo, M. and Vasserot, E., On the decomposition matrices of the quantized Schur algebra. Duke Math. J. 100(1999), no. 2, 267–297.Google Scholar
[31] Zwara, G., Degenerations for modules over representation-finite biserial algebras. J. Algebra 198(1997), no. 2, 563–581.Google Scholar