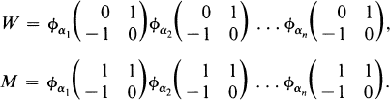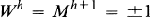Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ignatenko, V. F.
1991.
Geometric theory of invariants of groups generated by reflections.
Journal of Soviet Mathematics,
Vol. 55,
Issue. 6,
p.
2168.
Luzgarev, A.
Stepanov, A.
and
Vavilov, N.
2010.
Calculations in exceptional groups over rings.
Journal of Mathematical Sciences,
Vol. 168,
Issue. 3,
p.
334.


 be the universal Chevalley group ([
be the universal Chevalley group ([ over a field
over a field 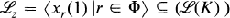 where Ф is the set of roots of
where Ф is the set of roots of