Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-23T07:34:21.787Z Has data issue: false hasContentIssue false
  • English
  • Français

Generating Functions for Hecke Algebra Characters

Published online by Cambridge University Press:  20 November 2018

Matjaž Konvalinka  and
Mark Skandera
Matjaž Konvalinka
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139, U.S.A. email: [email protected]
Mark Skandera
Affiliation:
Department of Mathematics, Lehigh University, Bethlehem, PA 18015, U.S.A. email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Certain polynomials in 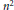${{n}^{2}}$ variables that serve as generating functions for symmetric group characters are sometimes called 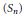$\left( {{S}_{n}} \right)$ character immanants. We point out a close connection between the identities of Littlewood–Merris–Watkins and Goulden–Jackson, which relate 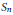${{S}_{n}}$ character immanants to the determinant, the permanent and MacMahon's Master Theorem. From these results we obtain a generalization of Muir's identity. Working with the quantum polynomial ring and the Hecke algebra ${{H}_{n}}\left( q \right)$, we define quantum immanants that are generating functions for Hecke algebra characters. We then prove quantum analogs of the Littlewood–Merris–Watkins identities and selected Goulden–Jackson identities that relate ${{H}_{n}}\left( q \right)$ character immanants to the quantum determinant, quantum permanent, and quantum Master Theorem of Garoufalidis–Lê–Zeilberger. We also obtain a generalization of Zhang's quantization of Muir's identity.

Keywords

15A1520C0881R50determinantpermanentimmanantHecke algebra characterquantum polynomial ring
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 63 , Issue 2 , 01 April 2011 , pp. 413 - 435
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Cartier, P. and Foata, D., Problèmes combinatoires de commutation et réarrangements. Lecture Notes in Mathematics, 85, Springer-Verlag, Berlin-New York, 1969.Google Scholar
[2] Curtis, C.W., On Lusztig's isomorphism theorem for Hecke algebras. J. Algebra 92(1985), no. 2, 348–365. doi:10.1016/0021-8693(85)90125-5Google Scholar
[3] Curtis, C.W., Iwahori, N., and Kilmoyer, R., Hecke algebras and characters of parabolic type of finite groups with (B, N)-pairs. Inst. Hautes Études Sci. Publ. Math. 40(1971), 81–116.Google Scholar
[4] Domokos, M. and Lenagan, T. H., Conjugation coinvariants of quantum matrices. Bull. London Math. Soc. 35(2003), no. 1, 117–127. doi:10.1112/S0024609302001650Google Scholar
[5] Douglass, J. M., An inversion formula for relative Kazhdan-Luszig polynomials. Comm. Algebra 18(1990), no. 2, 371–387. doi:10.1080/00927879008823919Google Scholar
[6] Foata, D. and Han, G.-N., A new proof of the Garoufalidis-Lê-Zeilberger quantum MacMahon master theorem. J. Algebra 307(2007), no. 1, 424–431. doi:10.1016/j.jalgebra.2006.04.032Google Scholar
[7] Foata, D. and Han, G.-N., Specializations and extensions of the quantum MacMahon Master Theorem. Linear Algebra Appl. 423(2007), no. 2–3, 445–455. doi:10.1016/j.laa.2007.01.019Google Scholar
[8] Foata, D. and Han, G.-N., A basis for the right quantum algebra and the “1 = q” principle. J. Algebraic Combin. 27(2008), no. 2, 163–172. doi:10.1007/s10801-007-0080-5Google Scholar
[9] Fulton, W., Young tableaux. With applications to representation theory and geometry. London Mathematical Society Student Texts, 35, Cambridge University Press, Cambridge, 1997.Google Scholar
[10] Gantmacher, F. R., The theory of matrices. Vol. 1, Chelsea, New York, 1959.Google Scholar
[11] Garoufalidis, S., Lê, T. T. Q., and Zeilberger, D., The quantum MacMahon master theorem. Proc. Natl. Acad. Sci. USA 103(2006), no. 38, 13928–13931 (electronic). doi:10.1073/pnas.0606003103Google Scholar
[12] Geck, M. and Pfeiffer, G., Characters of finite Coxeter groups and Iwahori-Hecke algebras. London Mathematical Society Monographs, New Series, 21, The Clarendon Press, Oxford University Press, New York, 2000.Google Scholar
[13] Goulden, I. P. and Jackson, D. M., Immanants of combinatorial matrices. J. Algebra 148(1992), no. 2, 305–324. doi:10.1016/0021-8693(92)90196-SGoogle Scholar
[14] Goulden, I. P. and Jackson, D. M., Immanants, Schur functions, and the MacMahon master theorem. Proc. Amer. Math. Soc. 115(1992), no. 3, 605–612.Google Scholar
[15] Greene, C., Proof of a conjecture on immanants of the Jacobi-Trudi matrix. Linear Algebra Appl. 171(1992), 65–79. doi:10.1016/0024-3795(92)90250-EGoogle Scholar
[16] Hai, P. H. and Lorenz, M., Koszul algebras and the quantum MacMahon master theorem. Bull. Lond. Math. Soc. 39(2007), no. 4, 667–676. doi:10.1112/blms/bdm037Google Scholar
[17] Haiman, M., Hecke algebra characters and immanant conjectures. J. Amer. Math. Soc. 6(1993), no. 3, 569–595.Google Scholar
[18] Humphreys, J. E., Reflection groups and Coxeter groups. Cambridge Studies in Advanced Mathematics, 29, Cambridge University Press, Cambridge, 1990.Google Scholar
[19] Konvalinka, M. and Pak, I., Non-commutative extensions of the MacMahon Master Theorem. Adv. Math. 216(2007), no. 1, 29–61. doi:10.1016/j.aim.2007.05.020Google Scholar
[20] Kostant, B., Immanant inequalities and 0-weight spaces. J. Amer.Math. Soc. 8(1995), no. 1, 181–186. doi:10.1090/S0894-0347-1995-1261291-7Google Scholar
[21] Krattenthaler, C. and Schlosser, M., A new multidimensional matrix inverse with applications to multiple q-series. Discrete Math. 204(1999), no. 1–3, 249–279. doi:10.1016/S0012-365X(98)00374-4Google Scholar
[22] Littlewood, D. E., The theory of group characters and matrix representations of groups. Oxford University Press, New York, 1940.Google Scholar
[23] Macdonald, I., Symmetric functions and Hall polynomials. Oxford Mathematical Monographs, The Clarendon Press, Oxford University Press, Oxford, 1979.Google Scholar
[24] MacMahon, P., Combinatory analysis. Vol. 1 and 2, Cambridge University Press, Cambridge, 1915.Google Scholar
[25] Merris, R. and W.Watkins, Inequalities and identities for generalized matrix functions. Linear Algebra Appl. 64(1985), 223–242. doi:10.1016/0024-3795(85)90279-4Google Scholar
[26] Schur, I., Über endliche Gruppen und Hermitesche Formen. Math. Z. 1(1918), no. 2–3, 184–207. doi:10.1007/BF01203611Google Scholar
[27] Schwinger, J., The theory of quantized fields. V. Physical Rev. (2) 93(1954), 615–628. doi:10.1103/PhysRev.93.615Google Scholar
[28] Stanley, R. P., Positivity problems and conjectures. In: Mathematics: frontiers and perspectives, American Mathematical Society, Providence, RI, 2000, pp. 295–319.Google Scholar
[29] Stembridge, J., Immanants of totally positive matrices are nonnegative. Bull. London Math. Soc. 23(1991), no. 5, 422–428. doi:10.1112/blms/23.5.422Google Scholar
[30] Stembridge, J., Some conjectures for immanants. Can. J. Math. 44(1992), no. 5, 1079–1099.Google Scholar
[31] Vere-Jones, D., Permanents, determinants, bosons and fermions. New Zealand Math. Soc. Newslett. 29(1983), 18–23.Google Scholar
[32] Vere-Jones, D., An identity involving permanents. Linear Algebra Appl. 63(1984), 267–270. doi:10.1016/0024-3795(84)90148-4Google Scholar
[33] Zhang, J. J., The quantum Cayley-Hamilton theorem. J. Pure Appl. Algebra 129(1998), no. 1, 101–109. doi:10.1016/S0022-4049(97)00039-XGoogle Scholar