Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T01:02:05.734Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized Variation and Functions of Slow Growth

Published online by Cambridge University Press:  20 November 2018

Robert D. Berman
Robert D. Berman*
Affiliation:
Wayne State University, Detroit, Michigan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Many of the basic results of HP theory on the disk Δ = {|z| < 1} are proved using the Cauchy-Stieltjes representation

1.1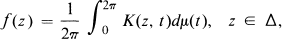

and the Poisson-Stieltjes representation

1.2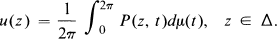

Here, μ:R → C is a complex-valued function of a real variable that is of bounded variation on [0, 2π] such that μ(t + 2π) = μ(t) + μ(2t) — μ(0), t ∊ R,

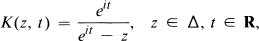
is the Cauchy kernel, and

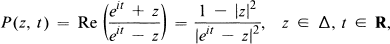
is the Poisson kernel. It is therefore natural to generalize these representations in such a way that some of the basic properties and results carry over. Such a generalization occurs when the assumption that μ is of bounded variation on [0, 2μ] is replaced by the requirement that it is measurable and bounded on [0, 2μ] (cf. [9]). The integrals in (1.1) and (1.2) are then defined by a formal integration by parts. After some preliminaries in Section 2, we catalogue a variety of results which remain valid in Section 3.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 40 , Issue 1 , 01 February 1988 , pp. 55 - 85
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Ahem, P., The mean modulus of the derivative of an inner function, Indiana Math. J.. 28 (1979), 311–347.Google Scholar
2. Berman, R. and Cohn, W., A radial Phragmén-Lindelôf theorem, Complex Variables, Theory and Application. 6 (1986), 299–307.Google Scholar
3. Berman, R. and Cohn, W., Tangential limits of Blaschke products and functions of bounded mean oscillation, Illinois J. Math. 31 (1987), 218–239.Google Scholar
4. Berman, R., Brown, L. and Cohn, W., Moduli of continuity and generalized BCH sets, Rocky Mountain J. Math. 17 (1987), 315–338.Google Scholar
5. Brudnyi, U. A. and Gopengauz, I. E., A generalization of a theorem of Hardy and Littlewood, Mat. Sb.. 52 (1960), 891–894.Google Scholar
6. Caveny, D. J. and Novinger, W. P., Boundary zeros of functions with derivative in hP', Proc. Amer. Math. Soc.. 25 (1970), 776–780.Google Scholar
7. Duren, P., Theory of Hp spaces (Academic Press, New York, 1970).Google Scholar
8. Goffman, C., Moran, G. and Waterman, D., The structure of regulated functions, Proc. Amer. Math. Soc. 57 (1976), 61–65.Google Scholar
9. Hayman, W. K. and Korenblum, B., An extension of the Riesz-Herglotz formula, Ann. Acad. Sci. Fenn. Ser. A I Math. 2 (1976), 175–201.Google Scholar
10. Heins, M., The minimum modulus of a bounded analytic functions, Duke Math. J. 14 (1947), 179–215.Google Scholar
11. Heins, M., Complex function theory (Academic Press, New York, 1968).Google Scholar
12. Kahane, J. P. and Salem, R., Ensembles parfaits et series trigonometriques (Hermann, Paris, 1963).Google Scholar
13. Musielak, J. and Orlicz, W., On generalized variation I, Studia Math. 18 (1959), 11–41.Google Scholar
14. Rogers, C. A., Hausdorff measures (Cambridge Univ. Press, 1970).Google Scholar
15. Rudin, W., Real and complex analysis, 2nd ed. (McGraw-Hill, New York, 1974).Google Scholar
16. Samuelsson, Â., On radial zeros of Blaschke products, Ark. Math. 7 (1968), 477–494.Google Scholar
17. Shapiro, H. S., Weakly invertible elements in certain function spaces and generators in l', Mich. Math. J.. 11 (1964), 161–165.Google Scholar
18. Shirokov, N. A., Zero sets for functions from Aw, Zap. Nauchn. Sem. Leningrad. Otdel. Math. Inst. Steklov. (LOMI) 707 (1982), 178–188, 232.Google Scholar
19. Zygmund, A., Trigonometric series, 2nd ed. (Cambridge, 1959).Google Scholar