Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-05T12:52:43.420Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized Spectral Theory in Complex Banach Algebras

Published online by Cambridge University Press:  20 November 2018

G. N. Hile  and
W. E. Pfaffenberger
G. N. Hile
Affiliation:
University of Hawaii, Honolulu, Hawaii
W. E. Pfaffenberger
Affiliation:
University of Victoria, Victoria, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A be an element of a complex Banach algebra 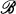with identitI. The ordinary spectrum of A, sp(A), consists of those points z in the complex plane such that A — zI has no inverse in 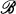. If Q is any other element of 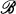, we define spQ(A), the spectrum of A relative to Q, or Q-spectrum of A, as those points z such that 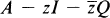has no inverse in 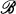. Thus if Q = 0 the Q-spectrum of A is the same as the ordinary spectrum of A.

The generalized notion of spectrum, spQ(A), retains many of the properties of the ordinary spectrum, particularly when A and Q commute and the ordinary spectrum of Q does not meet the unit circle. Under these conditions the Q-spectrum of A is a nonempty compact subset of the plane, and if both sp(A) and sp(Q) are finite (or countable), so is spQ(A).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 37 , Issue 6 , 01 December 1985 , pp. 1211 - 1236
Copyright
Copyright © Canadian Mathematical Society 1985

References

1. Goldschmidt, B., Funktionentheoretische eigenschaften verallgemeinerter analytischer vektoren, Math. Nachr. 90 (1979), 57–90.Google Scholar
2. Halmos, P. R., A Hilbert space problem book (Van Nostrand, Princeton, N.J., 1967).Google Scholar
3. Hile, G. N. and Pfaffenberger, W. E., The relative spectrum of elements in a real Banach algebra, Math. Ann. 250 (1980), 113–133.Google Scholar
4. Hile, G. N., Elliptic systems in the plane with first order term and constant coefficients, Comm. Partial Differential Equations 3 (1978), 949–977.Google Scholar
5. Hile, G. N., Function theory for generalized Beltrami systems, Contemporary Mathematics, Plane Ellipticity and Related Problems, Amer. Math. Soc. 11 (1982), 101–125.Google Scholar
6. Hille, E., Methods in classical and functional analysis (Addison-Wesley, Reading, Mass., 1972).Google Scholar
7. Kato, T., Perturbation theory for linear operators, 2nd ed. (Springer, New York, 1976).Google Scholar
8. Lorch, E. R., Spectral theory (Oxford University Press, New York, 1962).Google Scholar
9. Radjavi, H. and Rosenthal, P., Invariant subspaces, Ergebnisse der Mathematik und ihrer Grenzgebiete 77 (Springer-Verlag, Berlin, 1973).CrossRefGoogle Scholar
10. Rickart, C. E., General theory of Banach algebras, The University Series in Higher Mathematics (Van Nostrand, Princeton, N.J., 1960).Google Scholar