Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T00:23:56.689Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized Mellin Convolutions and their Asymptotic Expansions

Published online by Cambridge University Press:  20 November 2018

R. Wong  and
J. P. Mcclure
R. Wong
Affiliation:
University of Manitoba, Winnipeg, Manitoba
J. P. Mcclure
Affiliation:
University of Manitoba, Winnipeg, Manitoba
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A large number of important integral transforms, such as Laplace, Fourier sine and cosine, Hankel, Stieltjes, and Riemann- Liouville fractional integral transforms, can be put in the form

1.1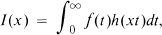

where f(t) and the kernel, h(t), are locally integrable functions on (0,∞), and x is a positive parameter. Recently, two important techniques have been developed to give asymptotic expansions of I(x) as x → + ∞ or x → 0+. One method relies heavily on the theory of Mellin transforms [8] and the other is based on the use of distributions [24]. Here, of course, the integral I(x) is assumed to exist in some ordinary sense.

If the above integral does not exist in any ordinary sense, then it may be regarded as an integral transform of a distribution (generalized function). There are mainly two approaches to extend the classical integral transforms to distributions.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 36 , Issue 5 , 01 October 1984 , pp. 924 - 960
Copyright
Copyright © Canadian Mathematical Society 1984

References

1. Durbin, P., Asymptotic expansion of Laplace transforms about the origin using generalized functions, J. Inst. Maths. Appl. 23 (1979), 181–192.Google Scholar
2. Erdélyi, A., Fractional integrals of generalized functions, J. Australian Math. Soc. 14 (1972), 30–37.Google Scholar
3. Erdélyi, A., Stieltjes transforms of generalized functions, Proc. Royal Soc. Edinburgh A 76 (1977), 221–249.Google Scholar
4. Erdélyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F., Higher transcendental functions, Vol. 1 (McGraw-Hill, New York, 1953).Google Scholar
5. Erdélyi, A. and McBride, A. C., Fractional integrals of distributions, SIAM J. Math. Anal. 1 (1970), 547–557.Google Scholar
6. Gelfand, I. M. and Shilov, G. E., Generalized functions, Vol 1 (Academic Press, New York, 1964).Google Scholar
7. Handelsman, R. A. and Lew, J. S., Asymptotic expansion of Laplace transforms near the origin, SIAM J. Math. Anal. 1 (1970), 118–130.Google Scholar
8. Handelsman, R. A. and Lew, J. S., Asymptotic expansion of a class of integral transforms with algebraically dominated kernels, J. Math. Anal. Appl. 35 (1971), 405–433.Google Scholar
9. Jeanquartier, P., Transformation de Mellin et développements asymptotiques, L'Enseignement Mathématique 25 (1979), 285–308.Google Scholar
10. Jones, D. S., Generalized transforms and their asymptotic behavior, Philos. Trans. Roy. Soc. London Ser. A 265 (1969), 1–43.Google Scholar
11. Jones, D. S., Infinite integrals and convolution, Proc. Roy. Soc. London, A 371 (1980), 479–508.Google Scholar
12. Jones, D. S., Generalized functions and their convolutions, Proc. Royal Soc. Edinburgh, 91 A (1982), 213–233.Google Scholar
13. Jones, D. S., The theory of generalized functions (Cambridge University Press, Cambridge, 1982).CrossRefGoogle Scholar
14. Lavoine, J., Sur de théorèmes abéliens et taubériens de la transformation de Laplace, Ann. Inst Henri Poincaré 4 (1966), 49–65.Google Scholar
15. Lavoine, J. and Misra, O. P., Théorèmes abéliens pour la transformation de Stieltjes des distributions, C. R. Acad. Sci. Paris 279 (1974), 99–102.Google Scholar
16. Lavoine, J. and Misra, O. P., Abelian theorems for the distributional Stieltjes transformation, Math. Proc. Camb. Phil Soc. 86 (1979), 287–293.Google Scholar
17. McBride, A. C., Fractional calculus and integral transforms of generalized functions, Research Notes in Mathematics 31 (Pitman, London, 1979).Google Scholar
18. McClure, J. P. and Wong, R., Explicit error terms for asymptotic expansions of Stieltjes transforms, J. Inst. Math. Appl. 22 (1978), 129–145.Google Scholar
19. McClure, J. P. and Wong, R., Exact remainders for asymptotic expansions of fractional integrals, J. Inst. Math. Appl 24 (1979), 139–147.Google Scholar
20. Rudin, W., Functional analysis (McGraw-Hill, New York, 1973).Google Scholar
21. Schwartz, L., Mathematics for physical sciences (Addison-Wesley, Reading, Mass., 1966).Google Scholar
22. Watson, G. N., A Treatise on the theory of Besselfunctions 2nd ed. (Cambridge University Press, Cambridge, 1944).Google Scholar
23. Wong, R., Explicit error terms for asymptotic expansions of Mellin convolutions, J. Math. Anal Appl. 72 (1979), 740–756.Google Scholar
24. Wong, R., Error bounds for asymptotic expansions of integrals, SIAM Rev. 22 (1980), 401–435.Google Scholar
25. Wong, R., Distributional derivation of an asymptotic expansion, Proc. Amer. Math. Soc. 80 (1980), 266–270.Google Scholar
26. Wong, R. and Wyman, M., A generalization of Watson's lemma, Can. J. Math. 24 (1972), 185–208.Google Scholar
27. Zayed, A. I., Asymptotic expansions of some integral transforms by using generalized functions, Trans. Amer. Math. Soc. 272 (1982), 785–802.Google Scholar
28. Zemanian, A. H., The distributional Laplace and Mellin transformations, SIAM J. Appl. Math 74 (1966), 41–59.Google Scholar
29. Zemanian, A. H., Generalized integral transformations (Interscience, New York, 1966).Google Scholar