Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T01:14:28.375Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized L(f) Spaces

Published online by Cambridge University Press:  20 November 2018

D. Hussein ,
M. A. Natsheh  and
I. Qumsiyeh
D. Hussein
Affiliation:
University of Jordan, Amman, Jordan
M. A. Natsheh
Affiliation:
University of Jordan, Amman, Jordan
I. Qumsiyeh
Affiliation:
University of Jordan, Amman, Jordan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given any set Γ, let 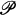be the family of all finite subsets of 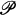. Let f:[0, ∞) → R satisfying: (1) f(x) = 0 if and only if x = 0, (2) f is increasing, (3) f(x + y) ≧ f(x) + f(y) for all x, y ≦ 0, and (4) f is continuous at zero from the right. Such an f is called a modules. Let C be the set of all moduli, and F = {fv ∊ C:v ∊ Γ). Q(Γ) will denote the set of all such F, s. For each F ∊ Q(Γ) let

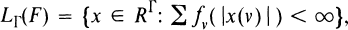
the summation is taken over Γ, and set

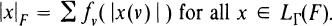
If Γ is countable Q(Γ) will be denoted by Q and LΓ(F) by L(F). Let

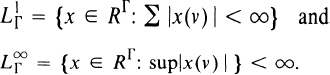
Note that

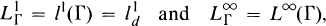
see [4, 5 and 6].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 37 , Issue 4 , 01 August 1985 , pp. 700 - 709
Copyright
Copyright © Canadian Mathematical Society 1985

References

1. Deeb, W., Necessary and sufficient conditions for the equality of L(f) and l1 , Can. J. Math. 34 (1982), 406–410.Google Scholar
2. Deeb, W. and Hussein, D., Results on L(f) spaces, The Arabian J. of Science and Engineering 5 (1980), 113–116.Google Scholar
3. Hussein, D. and Deeb, W., On the dual spaces of L(f), Dirasat, the Science Section, J. of the University of Jordan 6 (1979), 71–84.Google Scholar
4. Köthe, G., Topological vector spaces I (Springer Verlag, Berlin, 1969).Google Scholar
5. Köthe, G., Hebhare lokalkonvexe Raume, Math. Annalen 165 (1966), 181–195.Google Scholar
6. Ortynski, A., On complemented subspaces of Lp(Γ) for 0 < p ≧ 1, Bull Acad. Polon. Sci 26 (1978), 31–34.Google Scholar
7. Ruckle, W. H., FK spaces in which sequence of coordinate vectors is bounded. Can. J. Math. 25 (1973), 973–978.Google Scholar
8. Simons, S., The sequence spaces l(pv), m(pv), Proc. London Math. Soc. 15 (1965), 422–436.Google Scholar