Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T06:00:29.985Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized Kähler–Einstein Metrics andEnergy Functionals

Published online by Cambridge University Press:  20 November 2018

Xi Zhang  and
Xiangwen Zhang
Xi Zhang
Affiliation:
Department of Mathematics, University of Science and Technology of China, P. R. China. e-mail: [email protected]
Xiangwen Zhang
Affiliation:
Department of Mathematics, Columbia University, New York, NY 10027, USA. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract.

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

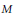In this paper, we consider a generalized Kähler–Einstein equation on a Kähler manifold $M$. Using the twisted 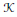$\mathcal{K}$–energy introduced by Song and Tian, we show that the existence of generalized Kähler–Einstein metrics with semi–positive twisting (1, 1)–form 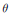$\theta$ is also closely related to the properness of the twisted 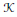$\mathcal{K}$-energy functional. Under the condition that the twisting form 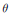$\theta$ is strictly positive at a point or 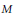$M$ admits no nontrivial Hamiltonian holomorphic vector field, we prove that the existence of generalized Kähler–Einstein metric implies a Moser–Trudinger type inequality.

Keywords

53C5532W20complex Monge–Ampère equationenergy functionalgeneralized Kähler–Einstein metricMoser–Trudinger type inequality
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 66 , Issue 6 , 01 December 2014 , pp. 1413 - 1435
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Aubin, T., Équation du type Monge–Ampère sur les variétés Kählerienes compactes. C. R. Acad. Sci.Paris Sér. A-B 283(1976), no. 3, Aiii, A119–A121.Google Scholar
[2] Aubin, T., Nonlinear analysis on manifolds, Monge–Amp`ere equations. Grundlehren der Mathematischen Wissenschaften, 252, Springer-Verlag, New York, 1982.Google Scholar
[3] Bando, S., The K–energy map, almost Einstein Kähler metrics and an inequality of the Miyaoka–Yau type. Tohuku Math. J. 39(1987), no. 2, 231–235.http://dx.doi.org/10.2748/tmj/1178228326 Google Scholar
[4] Bando, S. and Mabuchi, T., Uniqueness of Einstein–Kähler metrics modulo connected group actions. In: Algebraic geometry, Advanced Studies in Pure Math., 10, North-Holland, Amsterdam, 1987, pp. 11–40.Google Scholar
[5] Calabi, E., Extremal Kähler metrics. In: Seminar on differential geometry, Ann. of Math. Stud., 102, Princeton Univ. Press, Princeton, NJ, 1982, pp. 259–290.Google Scholar
[6] Cao, H. D., Deformation of Kähler metrics to Kähler–Einstein metrics on compact Kähler manifolds. Invent. Math. 81(1985), no. 2, 359–372.http://dx.doi.org/10.1007/BF01389058 Google Scholar
[7] Chen, X. and Tian, G., Geometry of K¨ahler metrics and foliations by holomorphic discs. Publ. Math.Hautes Études Sci. No. 107(2008), 1–107.Google Scholar
[8] Ding, W. Y., Remarks on the existence problem of positive Kähler–Einstein metrics. Math. Ann. 282(1988), no. 3, 463–471.http://dx.doi.org/10.1007/BF01460045 Google Scholar
[9] Ding, W. Y. and Tian, G., Kähler–Einstein metrics and the generalized Futaki invariant. Invent. Math. 110(1992), no. 2, 315–335.http://dx.doi.org/10.1007/BF01231335 Google Scholar
[10] Donaldson, S. K., Scalar curvature and stability of toric varieties. J. Differential Geom. 62(2002), no. 2, 289–349.Google Scholar
[11] Donaldson, S. K., Symmetric spaces, Kähler geometry and Hamiltonian dynamics. In: Northern California Symplectic Geometry Seminar, Amer. Math. Soc. Transl. Ser. 2, 196, Amer. Math. Soc., Providence, RI, 1999, pp. 13–33.Google Scholar
[12] Mabuchi, T., K–energy maps integrating Futaki invariants. Tohoku Math. J. 38(1986), no. 4, 575–593.http://dx.doi.org/10.2748/tmj/1178228410 Google Scholar
[13] Phong, D. H., Song, J., Sturm, J., and Weinkove, B., The Moser–Trudinger inequality on Kähler–Einstein manifolds. Amer. J. Math. 130(2008), no. 4, 1067–1085.http://dx.doi.org/10.1353/ajm.0.0013 Google Scholar
[14] Siu, Y. T., The existence of Kähler–Einstein metrics on manifolds with positive anticanonical line bundle and a suitable finite symmetry group. Ann. of Math. (2) 127(1988), no. 3, 585–627.http://dx.doi.org/10.2307/2007006 Google Scholar
[15] Song, J. and Tian, G., Canonical measures and Kähler–Ricci flow. J. Amer. Math. Soc. 25(2012), no. 2, 303–353.http://dx.doi.org/10.1090/S0894-0347-2011-00717-0 Google Scholar
[16] Stoppa, J., Twisted constant scalar curvature Kähler metrics and Kähler slope stability. J. Differential Geom. 83(2009), no. 3, 663–691.Google Scholar
[17] Székelyhidi, G., Greatest lower bounds on the Ricci curvature of Fano manifolds. Compos. Math. 147(2011), no. 1, 319–331.http://dx.doi.org/10.1112/S0010437X10004938 Google Scholar
[18] Tian, G., On Kähler–Einstein metrics on certain Kähler manifolds with C1(M)> 0. Invent. Math. 89(1987), no. 2, 225–246.http://dx.doi.org/10.1007/BF01389077 +0.+Invent.+Math.+89(1987),+no.+2,+225–246.http://dx.doi.org/10.1007/BF01389077>Google Scholar
[19] Tian, G., On Calabi's conjecture for complex surfaces with positive first Chern class. Invent. Math. 101(1990), no. 1, 101–172.http://dx.doi.org/10.1007/BF01231499 Google Scholar
[20] Tian, G., Kähler–Einstein metrics with positive scalar curvature. Invent. Math. 130(1997), no. 1, 1–37.http://dx.doi.org/10.1007/s002220050176 Google Scholar
[21] Tian, G. and Yau, S.-T., Kähler–Einstein metrics on complex surfaces with C,1> 0. Comm. Math. Phys. 112(1987), no. 1, 175–203.http://dx.doi.org/10.1007/BF01217685 +0.+Comm.+Math.+Phys.+112(1987),+no.+1,+175–203.http://dx.doi.org/10.1007/BF01217685>Google Scholar
[22] Tian, G. and Zhu, X., A nonlinear inequality of Moser–Trudinger type. Calc. Var. Partial Differential Equations 10(2000), no. 4, 349–354.http://dx.doi.org/10.1007/s005260010349 Google Scholar
[23] Yau, S. T., On the Ricci curvature of a compact Kähler manifold and the complex Monge–Ampère equation. Comm. Pure Appl. Math. 31(1978), no. 3, 339–411.http://dx.doi.org/10.1002/cpa.3160310304 Google Scholar
[24] Yau, S. T., Open problems in differential geometry. In: Chern—a great geometer of the twentieth century, Int. Press, Hong Kong, 1992, pp. 275–319.Google Scholar