Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-05T15:51:08.695Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized Factorization in Hardy Spaces and the Commutant of Toeplitz Operators

Published online by Cambridge University Press:  20 November 2018

Michael Stessin  and
Kehe Zhu
Michael Stessin
Affiliation:
Department of Mathematics, SUNY, Albany, New York 12222, USA, e-mail: [email protected]
Kehe Zhu
Affiliation:
Department of Mathematics SUNY, Albany, New York 12222, USA, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

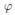Every classical inner function $\varphi$ in the unit disk gives rise to a certain factorization of functions in Hardy spaces. This factorization, which we call the generalized Riesz factorization, coincides with the classical Riesz factorization when 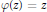$\varphi (z)\,=\,z$. In this paper we prove several results about the generalized Riesz factorization, and we apply this factorization theory to obtain a new description of the commutant of analytic Toeplitz operators with inner symbols on a Hardy space. We also discuss several related issues in the context of the Bergman space.

Keywords

47B3530D5547A15
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 55 , Issue 2 , 01 April 2003 , pp. 379 - 400
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Alexandrov, A. B., Multiplicity of boundary values of inner functions. Izv. Akad. Nauk Armyan. SSR Ser. Mat. (5) 22 (1987), 490–503, (Russian).Google Scholar
[2] Clark, D. N., One dimensional perturbations of restricted shifts. J. Analyse Math. 25 (1972), 169–191.Google Scholar
[3] Cowen, C., The commutant of an analytic Toeplitz operator. Trans. Amer.Math. Soc. 239 (1978), 1–31.Google Scholar
[4] Cowen, C. and MacCluer, B., Composition Operators on Spaces of Analytic Functions, CRC Press, 1995.Google Scholar
[5] Deddens, J. A. and Wong, T. K., The commutant of analytic Toeplitz operators. Trans. Amer.Math. Soc. 184 (1973), 261–273.Google Scholar
[6] Duren, P., Theory of Hp Spaces. Academic Press, New York, 1970.Google Scholar
[7] Halmos, P., Shifts on Hilbert spaces. J. Reine Angew.Math. 208 (1961), 102–112.Google Scholar
[8] Lance, T. and Stessin, M., Multiplication invariant subspaces of Hardy spaces. Canad. J. Math. 49 (1997), 100–118.Google Scholar
[9] Sz.-Nagy, B. and Foias, C., Harmonic Analysis of Operators on Hilbert Space. North-Holland, Amsterdam, 1970.Google Scholar
[10] Nordgren, E., Reducing subspaces of analytic Toeplitz operators. Duke Math. J. 34 (1967), 175–181.Google Scholar
[11] Stessin, M., Wold decomposition of the Hardy space and Blaschke products similar to a contraction. Colloq. Math. (2) 81 (1999), 271–284.Google Scholar
[12] Thomson, J., The commutant of certain analytic Toeplitz operators. Proc. Amer.Math. Soc. 54 (1976), 165–169.Google Scholar
[13] Zhu, K., Reducing subspaces for a class of multiplication operators. J. LondonMath. Soc. (2) 62 (2000), 553–568.Google Scholar