Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kirk, W. A.
1981.
Fixed Point Theory.
Vol. 886,
Issue. ,
p.
484.
Geremia, Raymond
and
Sullivan, Francis
1981.
Multi-dimensional volumes and moduli of convexity in banach spaces.
Annali di Matematica Pura ed Applicata,
Vol. 127,
Issue. 1,
p.
231.
Diminnie, Charles R.
1983.
A New Orthogonality Relation for Normed Linear Spaces.
Mathematische Nachrichten,
Vol. 114,
Issue. 1,
p.
197.
Bernal, Javier
and
Sullivan, Francis
1984.
Banach spaces that have normal structure and are isomorphic to a Hilbert space.
Proceedings of the American Mathematical Society,
Vol. 90,
Issue. 4,
p.
550.
Lin, Bor-Luh
and
Xin-Tai, Yu
1985.
On the K-uniform rotund and the fully convex Banach spaces.
Journal of Mathematical Analysis and Applications,
Vol. 110,
Issue. 2,
p.
407.
Yorke, A. C.
1985.
Rotundity redux.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 38,
Issue. 2,
p.
143.
Chao-Xun, Nan
and
Jian-Hua, Wang
1988.
On the Lk-UR and L-kR spaces.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 104,
Issue. 3,
p.
521.
Yu, Xin Tai
1988.
A geometrically aberrant Banach space with uniformly normal structure.
Bulletin of the Australian Mathematical Society,
Vol. 38,
Issue. 1,
p.
99.
Martínez-Yañez, C.
1989.
A fixed point theorem on k-uniformly rotund spaces.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 13,
Issue. 7,
p.
857.
Smith, Mark A.
and
Turett, Barry
1990.
Some examples concerning normal and uniform normal structure in Banach spaces.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 48,
Issue. 2,
p.
223.
Zheng, Liu
and
Ya-Dong, Zhuang
1990.
K-rotund complex normed linear spaces.
Journal of Mathematical Analysis and Applications,
Vol. 146,
Issue. 2,
p.
540.
Na, Qiyuan
1990.
ON FULLY CONVEX AND LOCALLY FULLY CONVEX BANACH SPACE.
Acta Mathematica Scientia,
Vol. 10,
Issue. 3,
p.
327.
Kutzarova, Denka
1991.
k-β and k-nearly uniformly convex Banach spaces.
Journal of Mathematical Analysis and Applications,
Vol. 162,
Issue. 2,
p.
322.
Tan, Kok-Keong
and
Xu, Hong Kun
1991.
On fixed point theorems of nonexpansive mappings in product spaces.
Proceedings of the American Mathematical Society,
Vol. 113,
Issue. 4,
p.
983.
Xu, Hong-Kun
1991.
Existence and convergence for fixed points of mappings of asymptotically nonexpansive type.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 16,
Issue. 12,
p.
1139.
Kutzarova, D.
Maluta, E.
and
Prus, S.
1992.
Property (β) implies normal structure of the dual space.
Rendiconti del Circolo Matematico di Palermo,
Vol. 41,
Issue. 3,
p.
353.
Kuczumow, Tadeusz
Reich, Simeon
and
Schmidt, Malgorzata
1993.
A fixed point property of 𝑙₁-product spaces.
Proceedings of the American Mathematical Society,
Vol. 119,
Issue. 2,
p.
457.
Lim, Teck-Cheong
and
Xu, Hong-Kun
1994.
Fixed point theorems for asymptotically nonexpansive mappings.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 22,
Issue. 11,
p.
1345.
Wang, Jianhua
1995.
MARTINGALE REPRESENTATION IN NEARLY UNIFORMLY CONVEX SPACES.
Acta Mathematica Scientia,
Vol. 15,
Issue. 3,
p.
352.
Lin, Pei-Kee
Tan, Kok-Keong
and
Xu, Hong-Kun
1995.
Demiclosedness principle and asymptotic behavior for asymptotically nonexpansive mappings.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 24,
Issue. 6,
p.
929.
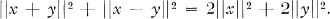
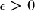

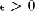 0 we have
0 we have 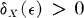 .
.


