Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T00:43:58.813Z Has data issue: false hasContentIssue false
  • English
  • Français

A Generalization of Degree Two Simple Finite-Dimensional Noncommutative Jordan Algebras

Published online by Cambridge University Press:  20 November 2018

Mary Ellen Conlon
Mary Ellen Conlon*
Affiliation:
Illinois Institute of Technology, Chicago, Illinois
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 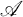be an algebra over a field 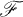. For x, y, z in 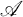, write (x, y, z) = (xy)z – x(yz) and x-y = xy + yx. The attached 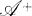algebra is the same vector space as 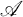, but the product of x and y is x · y. We aim to prove the following result.

THEOREM 1. Let 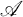be a finite-dimensional, power-associative, simple algebra of degree two over a field of prime characteristic greater than five. For all x, y, z in 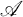, suppose

1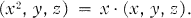

Then 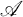is noncommutative Jordan.

The proof of Theorem 1 falls into three main sections. In § 3 we establish some multiplication properties for elements of the subspace 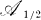in the Peirce decomposition 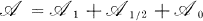. In §4 we construct an ideal of 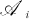which we then use to show that the nilpotent elements of 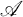form a subalgebra of 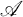for i = 0, 1.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 32 , Issue 2 , February 1980 , pp. 480 - 493
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Albert, A. A., A theory of power-associative commutative algebras, Trans. Amer. Math. Soc. 69 (1950), 503–527.Google Scholar
2. Anderson, C. T., On an identity common to Lie, Jordan, and quasias so dative algebras, Ph.D. thesis, Ohio State University (1964).Google Scholar
3. Florey, F. G., A generalization of noncommutative Jordan algebras, J. Algebr. 23 (1972), 502–518.Google Scholar
4. Goldman, J. I. and Kokoris, L. A., Generalized simple noncommutative Jordan algebras of degree two, J. Algebr. 42 (1976), 472–482.Google Scholar
5. Kosier, F., A generalization of alternative rings, Trans. Amer. Math. Soc. 112 (1964), 32–42.Google Scholar
6. Morgan, R. V. Jr., On a generalization of alternative rings, Can. J. Math. 22 (1970), 953–966.Google Scholar
7. Schafer, R. D., An introduction to nonassociative algebras (Academic Press, New York, 1966).Google Scholar