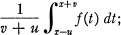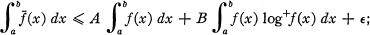Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rauch, H. E.
1956.
Harmonic and Analytic Functions Of Several Variables and The Maximal Theorem Of Hardy and Littlewood.
Canadian Journal of Mathematics,
Vol. 8,
Issue. ,
p.
171.
Stein, Elias M.
1958.
Localization and summability of multiple fourier series.
Acta Mathematica,
Vol. 100,
Issue. 1-2,
p.
93.
Yung-Ming, Chen
1958.
On a maximal theorem of Hardy and Littlewood and theorems concerning Fourier constants.
Mathematische Zeitschrift,
Vol. 69,
Issue. 1,
p.
418.
Stein, Elias M.
and
Weiss, Guido
1960.
On the theory of harmonic functions of several variables: I. The theory of Hp-spaces.
Acta Mathematica,
Vol. 103,
Issue. 1-2,
p.
25.
Chen, Yung-ming
1960.
Theorems of asymptotic approximation.
Mathematische Annalen,
Vol. 140,
Issue. 5,
p.
360.
Herz, C. S.
1961.
A maximal theorem.
Proceedings of the American Mathematical Society,
Vol. 12,
Issue. 2,
p.
229.
Phillips, Keith
1967.
The Maximal Theorems of Hardy and Littlewood.
The American Mathematical Monthly,
Vol. 74,
Issue. 6,
p.
648.
Gasper, George
1968.
On the Littlewood-Paley 𝑔-function and the Lusin 𝑠-function.
Transactions of the American Mathematical Society,
Vol. 134,
Issue. 3,
p.
385.
Phillips, Keith
1969.
Maximal functions for a class of locally compact noncompact groups.
Bulletin of the American Mathematical Society,
Vol. 75,
Issue. 2,
p.
384.
Stein, Elias M.
1970.
Boundary values of holomorphic functions.
Bulletin of the American Mathematical Society,
Vol. 76,
Issue. 6,
p.
1292.
Derrick, William R.
1971.
Inequalities forp-modules of curve families on Lipschitz surfaces.
Mathematische Zeitschrift,
Vol. 119,
Issue. 1,
p.
1.
Garnett, John B.
and
Latter, Robert H.
1978.
The atomic decomposition for Hardy spaces in several complex variables.
Duke Mathematical Journal,
Vol. 45,
Issue. 4,
Krantz, Steven G.
1979.
Analysis on the Heisenberg group and estimates for functions in hardy classes of several complex variables.
Mathematische Annalen,
Vol. 244,
Issue. 3,
p.
243.
Dyn'kin, E. M.
and
Osilenker, B. P.
1985.
Weighted estimates of singular integrals and their applications.
Journal of Soviet Mathematics,
Vol. 30,
Issue. 3,
p.
2094.
Slavin, Charles P
1989.
Properties of power series coefficients of H2(Π+) functions.
Journal of Mathematical Analysis and Applications,
Vol. 142,
Issue. 2,
p.
488.
Slavin, Charles P.
1990.
Poisson integrals and singular weights.
Journal of Mathematical Analysis and Applications,
Vol. 149,
Issue. 1,
p.
38.
Krantz, Steven G.
1991.
Invariant metrics and the boundary behavior of holomorphic functions on domains in $$\mathbb{C}^n $$.
Journal of Geometric Analysis,
Vol. 1,
Issue. 2,
p.
71.
Faridani, Adel
Ritman, Erik L.
and
Smith, Kennan T.
1992.
Local Tomography.
SIAM Journal on Applied Mathematics,
Vol. 52,
Issue. 2,
p.
459.
Berens, Hubert
and
Li, Luoqing
1993.
On the de la Vallée-Poussin Means on the Sphere.
Results in Mathematics,
Vol. 24,
Issue. 1-2,
p.
12.
Stoll, Manfred
2002.
Harmonic majorants for eigenfunctions of the Laplacian with finite Dirichlet integrals.
Journal of Mathematical Analysis and Applications,
Vol. 274,
Issue. 2,
p.
788.


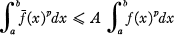
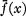 is defined as the supremum of the numbers
is defined as the supremum of the numbers